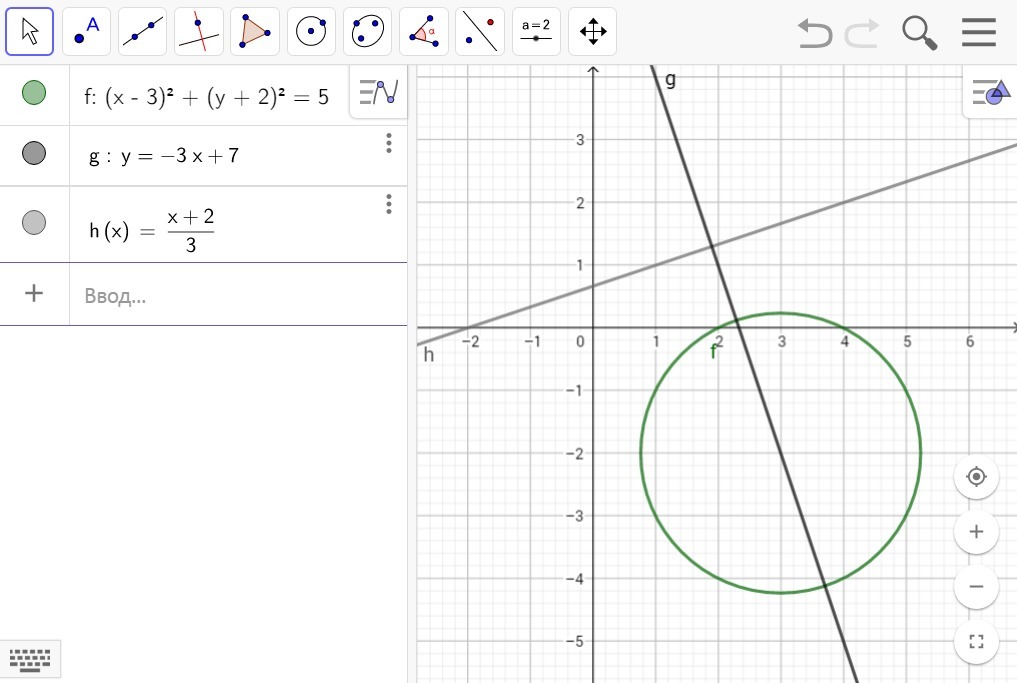
Найти уравнение прямой, содержащей диаметр окружности [tex] x^{2} + y^{2} -6x+4y+8=0[/tex], перпендикулярный прямой [tex]x-3y+2=0[/tex].

Перепишем уравнение прямой x + 2 = 3y:y = x/3 + 2/3.Здесь k1 = 1/3, b1 = 2/3.Перепишем уравнение окружности:x*x - 6x + 9 + y*y + 4y + 4 - 5 = 0,(x - 3)^2 + (y + 2)^2 = 5.Это окружность с радиусом, равным sqrt(5) (корень квадратный из пяти).Коеффициент k2 искомой функции, которая перпендикулярна к прямой x-3y+2=0 будет -(1/k1), т. е. -3.Искомая функция y3 = -3x + b2.Ее график проходит через центр окружности, координаты которого (3, -2), что мы получили из уравнения круга.y3 = -2 = -3*3 + b2 = -9 + b2b2 = 7Ответ: y3 = -3*x + 7