Задать вопрос Регистрация
Помочь другим

  • Помогите найти производные функций при заданном значении аргумента.

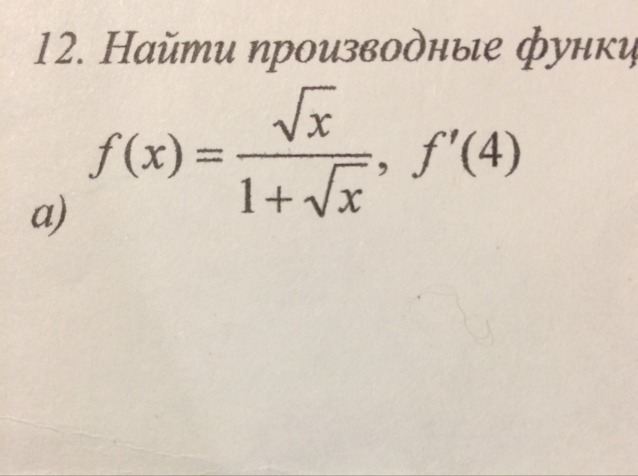
    question img

Ответы 1

  • найти производные функций при заданном значении аргумента f'(4)f(x)= \frac{ \sqrt{x}}{1+ \sqrt{x}} РешениеНайдем производную как производную дробиf(x)'= (\frac{ \sqrt{x}}{1+ \sqrt{x}})'=\frac{ (\sqrt{x})'(1+ \sqrt{x})- \sqrt{x} (1+ \sqrt{x} )'}{(1+ \sqrt{x})^2} = \frac{ \frac{1}{2 \sqrt{x} } (1+ \sqrt{x})- \sqrt{x} * \frac{1}{2 \sqrt{x} } }{(1+ \sqrt{x})^2} = \frac{ \frac{1}{2 \sqrt{x} } + \frac{1}{2}-\frac{1}{2} }{(1+ \sqrt{x})^2}= \frac{1}{2 \sqrt{x} (1+ \sqrt{x} )^2} Найдем значение производной при х = 4f'(4)= \frac{1}{2 \sqrt{4} (1+ \sqrt{4} )^2}= \frac{1}{2*2*(1+ 2 )^2}=\frac{1}{4*3^2}=\frac{1}{4*9}= \frac{1}{36} Ответ: f'(4) = 1/36

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years