Задать вопрос Регистрация
Помочь другим

  • найдите неопределенные интегралы,результаты проверить дифференцированием (под б)

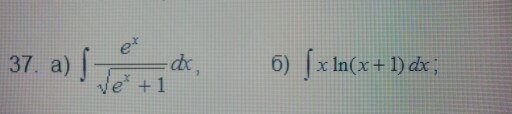
    question img

Ответы 1

  • \int\limits {xln(x+1)} \, dx Преобразуем подынтегральное выражение (можно и без этого, но мне показалось, что так проще).\int\limits {xln(x+1)} \, dx = \int\limits {(x+1-1)ln(x+1)} \, dx = \\ \\ \int\limits {(x+1)ln(x+1)} \, dx -\int\limits {ln(x+1)} \, dxСначала возьмём второй интеграл (по частям):\int\limits {ln(x+1)} \, dx = xln(x+1) - \int\limits { \frac{x}{x+1} } \, dx = xln(x+1) - \int\limits { \frac{x+1-1}{x+1} } \, dx = \\ \\ u = ln(x+1); du = \frac{dx}{x+1} \\ dv = dx; v = x \\ \\ =xln(x+1) - \int\limits { } \, dx + \int\limits { \frac{1}{x+1} } \, dx = xln(x+1) - x + ln(x+1) = \\ \\ = (x+1)ln(x+1) - xТеперь первый интеграл (тоже по частям):\int\limits {(x+1)ln(x+1)} \, dx = \frac{1}{2} (x+1)^2 ln(x+1) - \int\limits {\frac{1}{2} (x+1)^2} \frac{1}{x+1} \, dx = \\ \\ u = ln(x+1); du = \frac{dx}{x+1} \\ dv = x+1; v = \frac{1}{2} (x+1)^2 \\ \\ = \frac{1}{2} (x+1)^2 ln(x+1) - \frac{1}{2} \int\limits { (x+1)} \, dx = \\ \\ \frac{1}{2} (x+1)^2 ln(x+1) - \frac{1}{4} (x+1)^2 = \frac{1}{2} (x+1)^2 (ln(x+1) - \frac{1}{2})Собираем вместе, из первого вычитаем второй интеграл:\int\limits {xln(x+1)} \, dx = \\ \\ \frac{1}{2} (x+1)^2 (ln(x+1) - \frac{1}{2}) - (x+1)ln(x+1) + x + CПроверяем дифференцированием:(\frac{1}{2} (x+1)^2 (ln(x+1) - \frac{1}{2}) - (x+1)ln(x+1) + x)' = \\ \\ \frac{1}{2} 2(x+1)(ln(x+1) - \frac{1}{2}) + \frac{1}{2} (x+1)^2 \frac{1}{x+1} - \\ \\ -ln(x+1) -(x+1) \frac{1}{x+1}+1 = \\ \\ = (x+1)(ln(x+1) - \frac{1}{2})+ \frac{1}{2} (x+1) - ln(x+1) -1 + 1 = \\ \\ = (x+1)ln(x+1) -\frac{1}{2}(x+1) + \frac{1}{2} (x+1)- ln(x+1) = \\ \\ = xln(x+1) +ln(x+1)- ln(x+1) = xln(x+1)

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years