Задать вопрос Регистрация
Помочь другим

  • Найти производную, помогите, пожалуйста, в задании г) степень 1/х. Онлайн калькулятор не поможет, нужно полное решение.

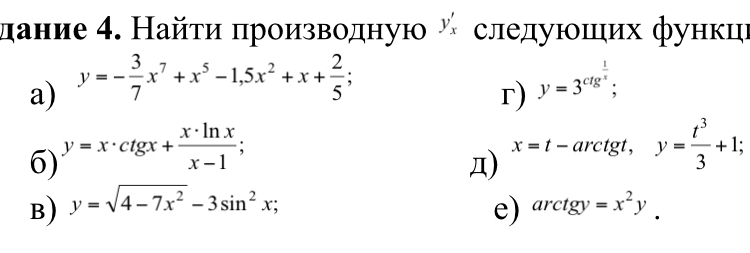
    question img

Ответы 2

  • Спасибо, огромное
  • 1)\; \; y=-\frac{3}{7}\, x^7+x^5-1,5\, x^2+x+\frac{2}{5}\\\\y'=-\frac{3}{7} \cdot 7x^6+5x^4-1,5\cdot 2x+1=-3x^6+5x^4-3x+1\\\\2)\; \; y=x\cdot ctgx+\frac{x\cdot lnx}{x-1}\\\\y'=ctgx+x\cdot \frac{-1}{sin^2x}+\frac{(lnx+x\cdot \frac{1}{x})(x-1)-x\cdot lnx\cdot 1}{(x-1)^2}=\\\\=ctgx-\frac{x}{sin^2x}+\frac{(lnx+1)(x-1)-x\cdot lnx}{(x-1)^2}\\\\3)\; \; y= \sqrt{4-7x^2}-3sin^2x\\\\y'= \frac{1}{2 \sqrt{4-7x^2}}\cdot (-7\cdot 2x) -3\cdot 2\cdot sinx\cdot cosx=- \frac{14x}{\sqrt{4-7x^2}}-3\cdot sin2x4)\; \; y=3^{ctg\frac{1}{x}}\\\\y'=3^{ctg\frac{x}{y}}\cdot \frac{-1}{sin^2 \frac{1}{x}}\cdot \frac{-1}{x^2}=3^{ctg\frac{x}{y}}\cdot \frac{1}{x^2\cdot sin^2\frac{1}{x}}\\\\5)\; \; \left \{ {{x=t-arctgt} \atop {y=\frac{t^3}{3}+1}} ight. \\\\x'_{t}=1-\frac{1}{1+t^2}=\frac{1+t^2-1}{1+t^2}=\frac{t^2}{1+t^2}\; \; ,\; \; y'_{t}= \frac{1}{3}\cdot 3t^2=t^2\\\\y'_{x}=\frac{y'_{t}}{x'_{t}}=\frac{t^2}{\frac{t^2}{1+t^2}}=1+t^26)\; \; arctgy=x^2y\\\\ \frac{y'}{1+y^2}=2xy+x^2\cdot y'\\\\y'\cdot ( \frac{1}{1+y^2}-x^2 )=2xy\\\\y'\cdot \frac{1-x^2(1+y^2)}{1+y^2} =2xy\\\\y'= \frac{2xy(1+y^2)}{1-x^2(1+-y^2)}

    • Автор:

      macyfwia
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years