-
Задание № 3
Если двухзначное число разделить на сумму его цифр, то в частном получится 3 и в остатке 7. Если затем взять сумму квадратов цифр этого числа и вычесть из нее произведение тех же цифр, то получится первоначальное число. Найти это число.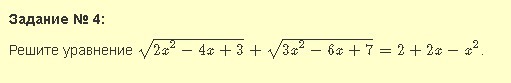
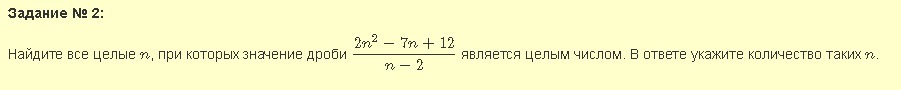

-
Предмет:
Математика -
Автор:
hutchinson - 5 лет назад
-
Ответы 2
-
Выяснил, как решить 4 задание. Дайте исправить!
-
Автор:
calliejacobs - 5 лет назад
-
0
-
-
Задание 2.
Это число будет целым, когда дробь 6/(n-2) будет целым числом.То есть, когда число (n-2) будет делителем числа 6.n - 2 = +-1; +-2; +-3; +-6.n = -4; -1; 0; 1; 3; 4; 5; 8Всего 8 значений n.Задание 3Обозначим двузначное число 10a + b. Сумма цифр тогда будет a + b.10a + b = 3(a + b) + 7a^2 + b^2 - ab = 10a + bИз 1 уравнения10a + b = 3a + 3b + 77a = 2b + 7b = 7(a - 1)/2Так как b - целое, то a - 1 должно делиться на 2.1) a - 1 = 0; a = 1; b = 7*0/2 = 0; 10a + b = 10Подставляем во 2 уравнение1^2 + 0^2 - 1*0 = 1 - не подходит.2) a - 1 = 2; a = 3; b = 7*2/2 = 7; 10a + b = 37Подставляем во 2 уравнение3^2 + 7^2 - 3*7 = 9 + 49 - 21 = 37 - подходит.3) a - 1 = 4; a = 5; b = 7*4/2 = 14 - не подходит.4) a - 1 = 6; a = 7; b = 7*6/2 = 21 - не подходит.5) a - 1 = 8; a = 9; b = 7*8/2 = 28 - не подходит.Ответ: 37Задание 4.
Область определения:{ 2x^2 - 4x + 3 >= 0{ 3x^2 - 6x + 7 >= 0{ -x^2 + 2x + 2 >= 0Находим дискриминанты{ D/4 = 4 - 2*3 = -2 < 0 - неравенство выполнено при любом x{ D/4 = 9 - 3*7 = -12 < 0 - неравенство выполнено при любом x{ D/4 = 1 - (-1)*2 = 3x1 = (-1 - √3)/(-1) = 1 + √3; x2 = (-1 + √3)/(-1) = 1 - √3x ∈ [1 - √3; 1 + √3]Решаем само уравнение
Для левой части будет минимальное значение √1 + √4 = 1 + 2 = 3 при x = 1.Для правой части будет максимальное значение 3 при том же x = 1.То есть эти части равны друг другу только в одной точке:x = 1
-
Автор:
dorotea - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Обсудите В какие три группы можно распределить данные имена существительные в город Курск шофер шорты сметана пшеница грабли мед учитель ножницы Север свекла Жмурки ешь петух
-
Предмет:
Русский язык -
Автор:
casey72 - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
стоимОстью, надо проверить букву О.
-
Предмет:
Русский язык -
Автор:
sherlyn - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
какой не должен быть спортсмен?
-
Предмет:
Русский язык -
Автор:
hinton - 5 лет назад
-
Ответов:
3 -
Смотреть
-
-
верно ли что всякое число, кратное 10, являются составным
-
Предмет:
Математика -
Автор:
xena8eih - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
