Задать вопрос Регистрация
Помочь другим

  • Вычислить значение производной сложной функции u=u(x,y), где x=x(t), y=y(t), при t=t0 с точностью до двух знаков после запятой:

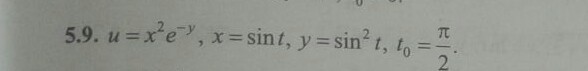
    question img

Ответы 4

  • https://znanija.com/task/27479232

    • Автор:

      angel71
    • 5 лет назад
    • 0
  • Можете вы решить это

    • Автор:

      tuckggso
    • 5 лет назад
    • 0
  • помогите, если не трудно
  • 5.9.u=x^2 * e^{-y} \\ x=sint \\ y = sin^2 t \\ \\ u = sin^2 t * e^{-sin^2 t} \\ \\ \frac{du}{dt} = (sin^2 t)' * e^{-sin^2 t} +sin^2 t * (e^{-sin^2 t} )' = \\ \\ = 2*sint*cost*e^{-sin^2 t}+ sin^2 t *e^{-sin^2 t}*(-2*sint)*cost = \\ \\ = 2*sint*cost*e^{-sin^2 t}*(1-sin^2 t) = \\ \\ = 2*sint*cos^3t*e^{-sin^2 t} \\ \\ sint_0 = sin \frac{ \pi }{2} = 1 \\ cost_0 = cos \frac{ \pi }{2} \\ \\ \frac{du}{dt} (t_0) = 2*1*0^3 *e^{-1} = 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years