Задать вопрос Регистрация
Помочь другим

  • 1. Вычислить значения частных производных f’x (M0), f’y (M0), f’z (M0) для данной функции f (x,y,z) в точке M0 (x0,y0,z0) с точностью до двух знаков после запятой.

    2. Вычислить значение производной сложной функции u=u(x,y), где x=x(t), y=y(t), при t=t0 с точностью до двух знаков после запятой.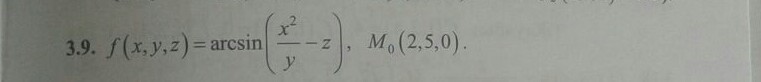

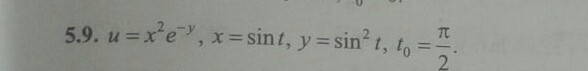
    question img
    question img

Ответы 6

  • я еще раз перепроверил через калькулятор, получаются те же числа, которые отличны от ваших

    • Автор:

      taniawaek
    • 4 года назад
    • 0
  • но в общем, если у вас другие ответы, то я задачу неправильно решил, а как иначе ее решать - понятия не имею

    • Автор:

      nadia
    • 4 года назад
    • 0
  • Ладно тогда, спасибо вам.
  • Просто ответы так написаны в книге
  • еще раз спасибо
  • 1) f(x,y,z)=arcsin( \frac{x^2}{y} - z)f'_x= \frac{1}{ \sqrt{1-(\frac{x^2}{y} - z)} } * \frac{2x}{y} f'_x(M_0)=\frac{1}{ \sqrt{1-(\frac{2^2}{5} - 0)} } * \frac{2*2}{5} = \frac{4}{5}* \frac{1}{ \sqrt{1- \frac{4}{5} } } = \frac{4}{5}* \frac{1}{ \sqrt{\frac{1}{5} } } =0.8*2.2361=1.79f'_y= \frac{1}{ \sqrt{1-(\frac{x^2}{y} - z)} } * (-\frac{x^2}{y^2} )f'_y(M_0)=\frac{1}{ \sqrt{1-(\frac{2^2}{5} - 0)} } * (-\frac{2^2}{5^2} )= \frac{1}{ \sqrt{ \frac{1}{5} } } * (-\frac{4}{25} )=-0.16*2.2361=-0.36f'_z=-\frac{1}{ \sqrt{1-(\frac{x^2}{y} - z)} }f'_z(M_0)=-\frac{1}{ \sqrt{1-(\frac{2^2}{5} - 0)} }= \frac{1}{ \sqrt{ \frac{1}{5} } } =2.242) u=x^2e^{-y}=sin^2t*e^{-sin^2t}u'=2sint*cost*e^{-sin^2t}-2sint*cost*e^{-sin^2t}*sin^2t==2sint*cost*e^{-sin^2t}(1-sin^2t)=2sint*cost*e^{-sin^2t}*cos^2t==2sint*cos^3t*e^{-sin^2t}u'(t_0)=2sin( \frac{ \pi }{2} )*cos^3(\frac{ \pi }{2} )*e^{-sin^2(\frac{ \pi }{2} )}=2*1*0*e^{-1}=0

    • Автор:

      josafat
    • 4 года назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years