-
Найдите все значения параметра а, при каждом из которых система имеет более двух решений.
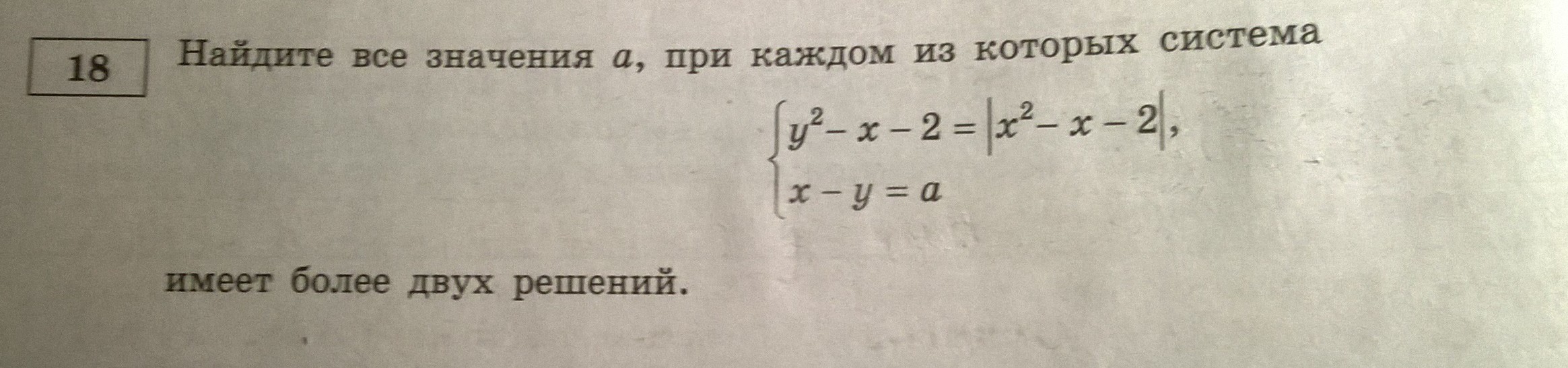
-
Предмет:
Математика -
Автор:
frederick10 - 5 лет назад
-
Ответы 2
-
Где-то ошибка, но где ... Спасибо вам большое за ваше решение. Но я же просто приравнял функцию окружности к функции прямой. Дискриминант =0, так как нам необходимо вычислить касательную и нашел значение а. Ответ: 1-корень из10 <a<-2 и a=0.
-
Автор:
gerardo744 - 5 лет назад
-
0
-
-
Ваше задание не слабо потрепало мне нервишки, тем не менее... результат есть.1) Рассмотрим первое уравнение системы, заранее разложим подмодульное выражение на множители и будем строить кусочно наш график на разных интервалах при том или ином раскрытие модуля.y^2-x-2=|(x+1)(x-2)|И так. раскроем данное выражение сначала с плюсом, и строим его график на области определение (-∞;-1) ∪ (2;+∞)y^2-x-2-x^2+x+2=0y=|x|, данное уравнение задаёт галочку в центре координат, но нам необходима только её часть, на промежутке описанном выше, далее раскрываем модуль и строим часть график на области (-1;2)y^2+x^2-2x+1-1-4=0y^2+(x-1)^2=5Данное уравнение задаёт окружность, а точнее в нашем случае часть дуги на области (-1;2) , причем легко заметить что данная дуга пересекает наш график в критических точках , а именно (-1;1) и (2;2) , и общий график функции будет выглядеть как показано на рисунке.Теперь разберёмся с 2-ым уравнение системы.Данное уравнение задаёт прямую, а точнее биссектрису прямоугольных координат , которая в зависимости от параметра двигается по оси ординат вверх или вниз, наша задача, её сдвинуть так, чтобы у нас было более 2-ух точек пересечения с графиком (более 2-ух решений) , это очевидно возможно , если графики функций будут расположены между точками (0;2) и неизвестной нам точки, когда прямая касается дуги нашей окружности , прямая проходит через точку ( 0;2),откуда a=0-2=a ; a=-2Теперь найдём тот случай когда прямая касается дуги, это сложнее, выразим из уравнение круга y. методом преобразований ясно что y=√(-x^2+2x+4) , чтобы найти абсциссу точки касание необходимо преровнять производную функции и производную нашей прямой, находим производную функции y`=(-x^2+2x+4)` = (-x+1)/√(-x^2+2x+4) , приравниваем её к производной прямой y`=(x+a)`=1(-x+1)=√(-x^2+2x+4) , возводим обе части в квадрат и обычными преобразованиями находим, что-4x=3x=-3/4Теперь найдём ординату подставь значение x в уравнение окружности.y=√(5-(49/16))= √31/4Теперь найдём значение параметра a=-√31/4-3/4Таким образом легко заключить вывод, что уравнение имеет более 2-ух решение если a ∈ (-2;-√31/4-3/4) , граничные точки не включаем т.к в них система имеет 2 решения.

-
Автор:
milo77hz - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
На чемпионате команды встречались со всеми другими по одному разу. Сколько было команд, если они провели 78 встреч?
-
Предмет:
Алгебра -
Автор:
alexusmoore - 5 лет назад
-
Ответов:
4 -
Смотреть
-
-
На экзамене 25 билетов по истории 5 из них по теме Александра 2 какова вероятность что ученику не достанется билет по теме Александра 2
-
Предмет:
Математика -
Автор:
figaro - 5 лет назад
-
Ответов:
0 -
Смотреть
-
-
найти сумму целых чисел от 1 до 200 которые заканчиваются на 5 и на 0. Паскаль
-
Предмет:
Информатика -
Автор:
amiracannon - 5 лет назад
-
Ответов:
0 -
Смотреть
-
- Периметр ромба равен 80см , одна из его диагоналей равна 24см Вычислите длину второй диагонали
How much to ban the user?
1 hour
1 day
100 years
