-
Вопрос по дифференциальным уравнением
Помогите пожалуйста!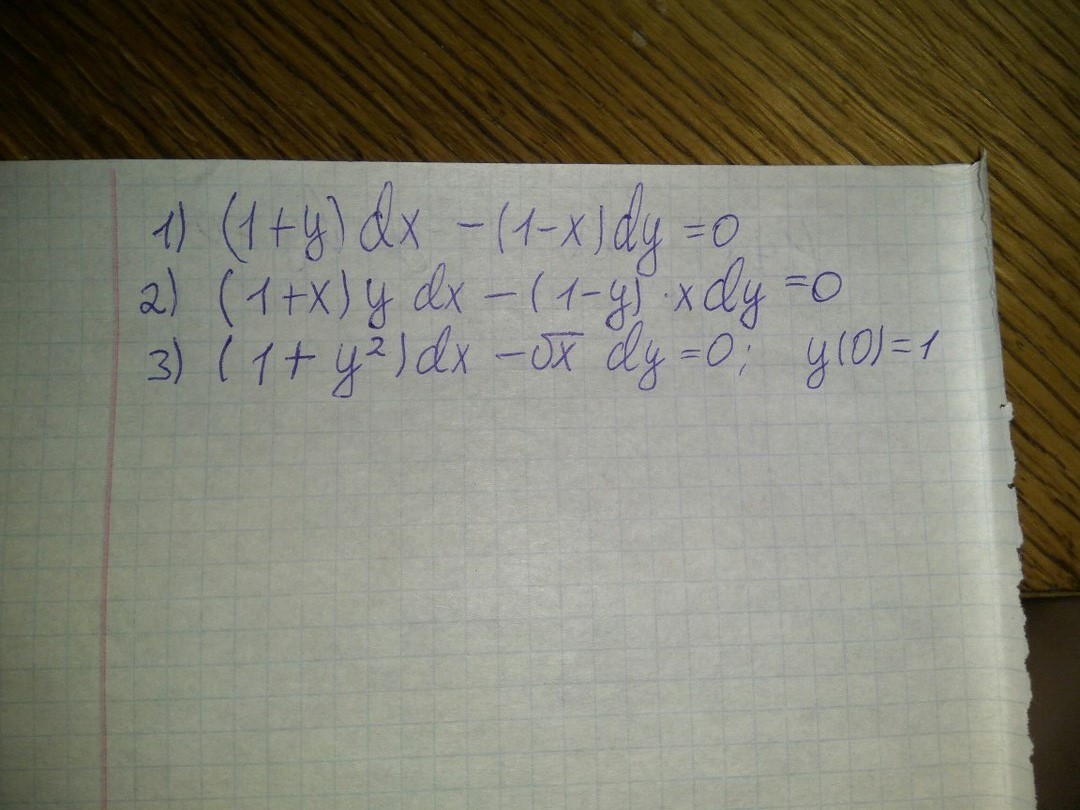
-
Предмет:
Математика -
Автор:
melany - 6 лет назад
-
Ответы 1
-
1)
2)
3)
-
Автор:
victoriatownsend - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Какую функцию выполняет спиной пловник у рыбы
-
Помогите, пожалуйста, с 22 -ым вопросом по географии.
-
Предмет:
География -
Автор:
furballzkxl - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Нашли на ветках два ГАЙНА
Что такое гайн????????
пожалуйста помогииитее
-
Предмет:
Русский язык -
Автор:
marianocraig - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите вычислить: Б) 25^4*5/125^3 в) 128^5/32^4*64^2 г) 6^12/(2^5*3^7)^2 д) 21^8/9^7*7^9
е) 125^3*81^2/15^10 ж) 0,125^12*2^37 з) (1/3) ^17*81^4 и) (3/5)^27*(125/27)^8
How much to ban the user?
1 hour
1 day
100 years
