-
Помогите, пожалуйста, решить неравенство (подробно и пошагово)
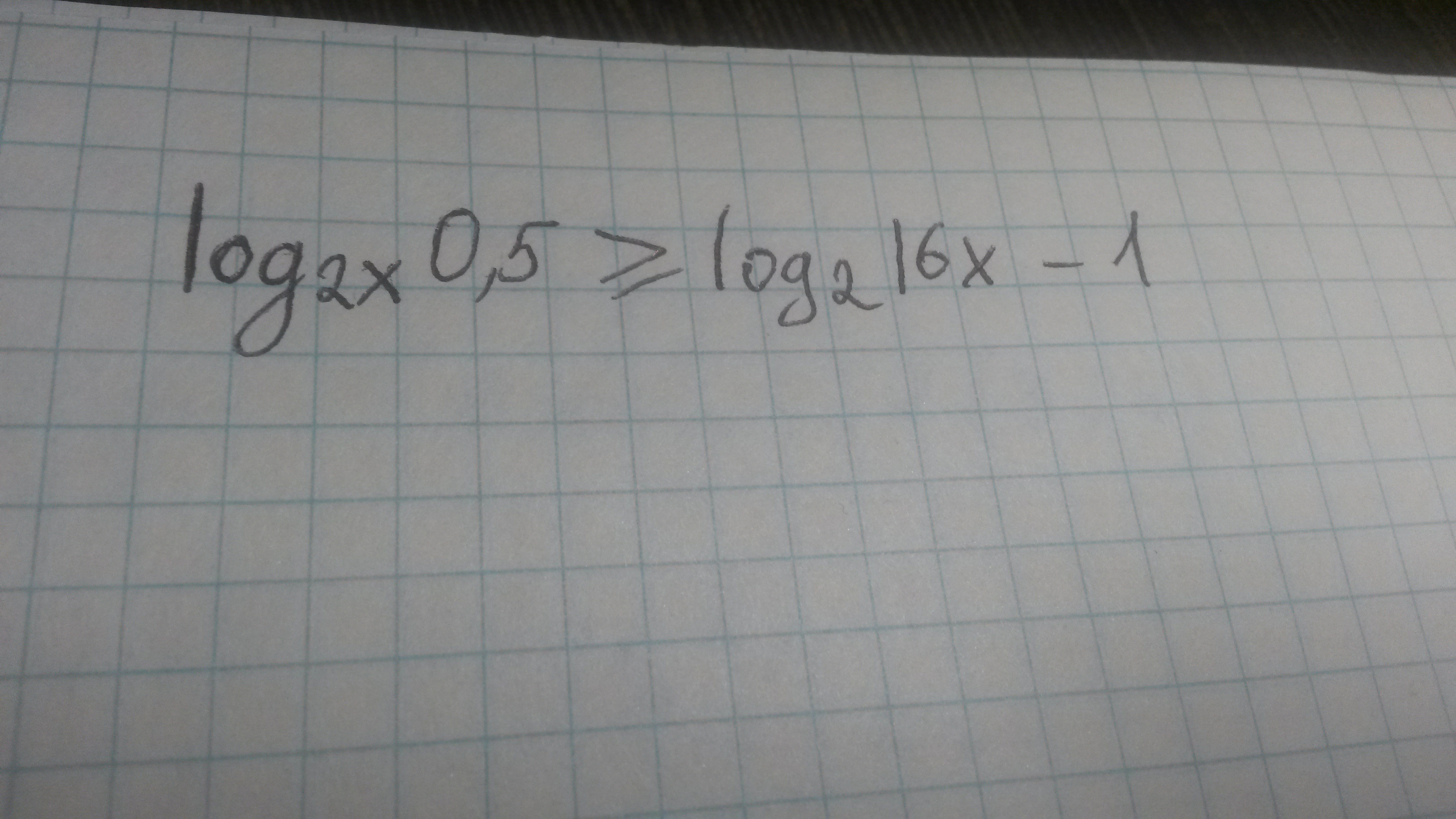
-
Предмет:
Математика -
Автор:
mattie75 - 6 лет назад
-
Ответы 1
-
Область определения логарифма: выражение под логарифмом положительно. Основание логарифма положительно и не равно 1.x > 0; x =/= 1/2.У логарифмов есть свойство:log_a (b) = 1/log_b (a)Поэтому log_(2x) (0,5) = 1/log_(0,5) (2x) = -1/log_2 (2x)Подставляем-1/log_2 (2x) >= log_2 (16x) - 10 >= log_2 (16) + log_2 (x) - 1 + 1/(log_2 (x)+1)Замена log_2 (x) = y4+y-1 + 1/(y+1) <= 0((y+3)(y+1) + 1) / (y+1) <= 0(y^2+4y+4) / (y+1) <= 0(y+2)^2 / (y+1) <= 0Оно равно 0 при y=log_2 (x) =2; x=2^2=4.При всех остальных y=/=-1 числитель положителен, поэтомуy+1 < 0; y=log_2 (x) < -1; x < 1/2С учётом обл. ОпределенияОтвет: x € (0; 1/2) U [4]
-
Автор:
howard - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
15 европейских стран и их столицы
-
Предмет:
География -
Автор:
oakleye7sx - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
на стороне BC прямоугольника ABCD отметьте точку P такую что AP=15 см.BA=12 см,PC=6 см.Нацдите площадь четырехугольника APCD
-
Предмет:
Геометрия -
Автор:
sophie67t6 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
1.Упростите выражение sin(п+а)
Варианты ответов
А.cos a. Б.sin a
B.-sin a. Г.- соs a.
2.Значение числа пи в градусах равно
А.360°. Б.270°.
В.180°. Г.90°.
3.на какой угол нужно повернуть точку Р(1;0),чтобы получить точку (0;-1)
А.17п\2. Б.-270°
В.630°. Г.п\3
-
Предмет:
Математика -
Автор:
mcgrath - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Решите пожалуйста столбиком.
1634/4,13851/57,27323/89.-
Предмет:
Математика -
Автор:
tituscarrillo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
