Задать вопрос Регистрация
Помочь другим

  • как найти помогите ! решил не знаю правильно или нет

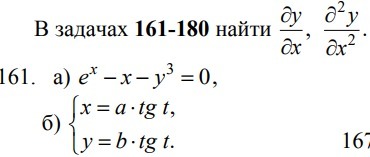
    question img

Ответы 2

  • Огромное спасибо!!! Во втором задание я допустил ошибку.
  • 1)\; \; e^{x}-x-y^{3}=0\; \; ,\; \; y^3=e^{x}-x \\\\y= \sqrt[3]{e^{x}-x} \\\\y'=\frac{1}{3}\cdot (e^{x}-x)^{-\frac{2}{3}}\cdot (e^{x}-1)= \frac{e^{x}-1}{3\cdot \sqrt[3]{(e^{x}-x)^2}}\\\\y''= \frac{1}{3}\cdot (-\frac{2}{3})\cdot (e^{x}-x)^{-\frac{5}{3}}\cdot (e^{x}-1)^2+\frac{1}{3}\cdot (e^{x}-x)^{-\frac{2}{3}}\cdot e^{x}=\\\\=- \frac{2(e^{x}-1)^2}{9\sqrt[3]{(e^{x}-x)^5}}+\frac{e^{x}}{3\cdot \sqrt[3]{(e^{x}-x)^2}}2)\; \; \left \{ {{x=a\cdot tgt} \atop {y=b\cdot tgt}} ight. \; \; ,\; \; a,b=const\\\\x'_{t}=\frac{a}{cos^2t}\; \; ,\; \; \; y'_{t}=\frac{b}{cos^2t}\\\\y'_{x}= \frac{y'_{t}}{x'_{t}}= \frac{b}{a}\\\\y''_{tt}=\frac{y''_{xx}}{x'_{t}}= \frac{0}{a/cos^2t} =0

    • Автор:

      gallagher
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years