-
Математика 11 класс, помогите пожалуйста! Спасибо!
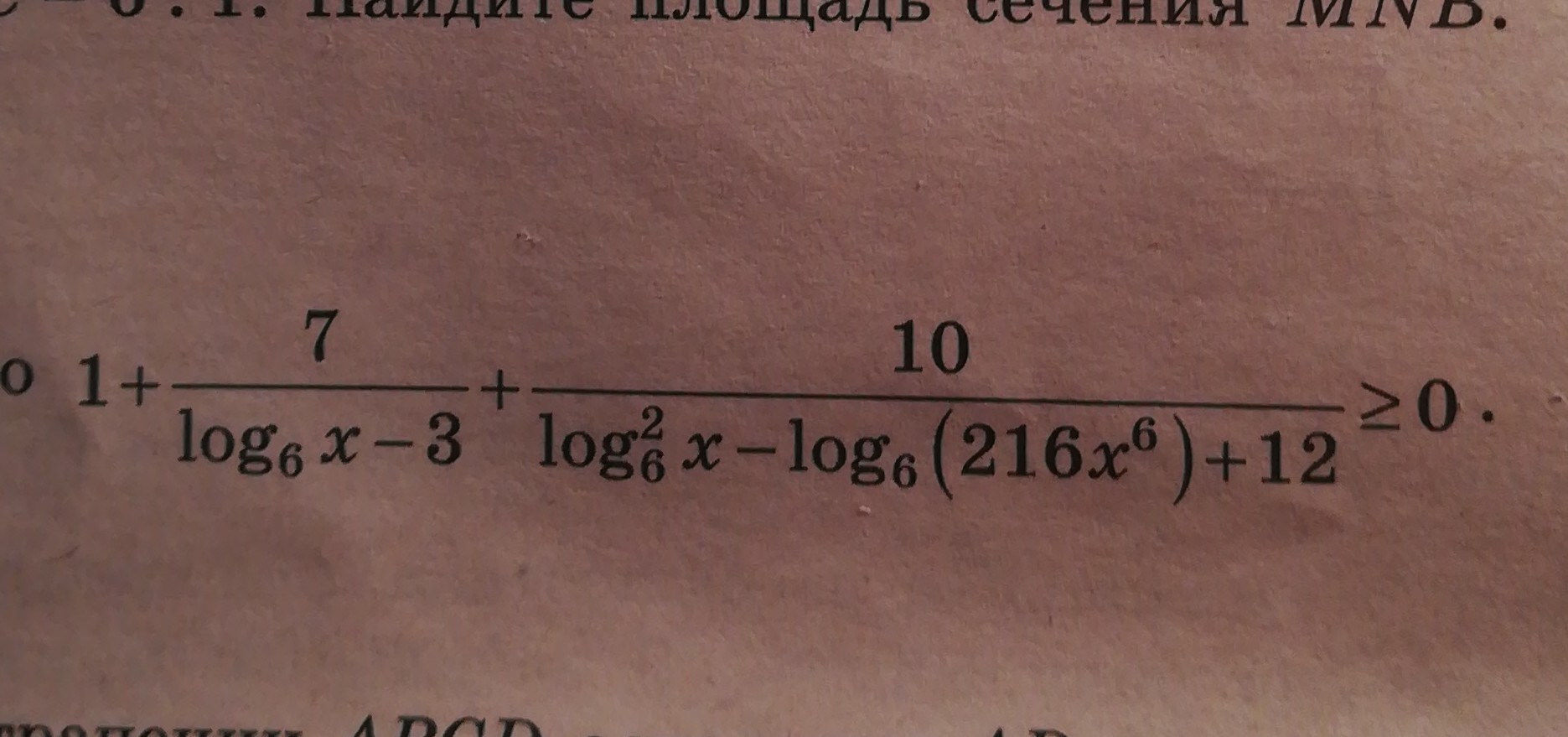
-
Предмет:
Математика -
Автор:
kramer9lcb - 5 лет назад
-
Ответы 1
-
Дано неравенство:
Определяем ОДЗ: - по свойству логарифмов х > 0, - (log_6(x) - 3) ≠ 0, x ≠ 6³ ≠ 216.Произведём замену:
Упростим знаменатель второй дроби.Заменим логарифм произведения на сумму логарифмов.216 = 6³.log_6(216x^6) = log_6(6³) + 6log_6(x) = 3 + 6y.Тогда знаменатель второй дроби примет вид: у²- (3 + 6у) + 12 = = у² - 6у + 9 или это (у - 3)².Исходное выражение теперь равно:
Если привести к общему знаменателю и сделать замену у-3 = z, то приравняв числитель полученного выражения нулю, получаем квадратное уравнение:z^2 + 7z + 10 = 0.Квадратное уравнение, решаем относительно z: Ищем дискриминант:D=7^2-4*1*10=49-4*10=49-40=9;Дискриминант больше 0, уравнение имеет 2 корня:z_1=(√9-7)/(2*1)=(3-7)/2=-4/2=-2;z_2=(-√9-7)/(2*1)=(-3-7)/2=-10/2=-5.Обратная замена: y = z +3 = -2 + 3 = 1, y = -5 + 3 = -2.Ещё одна замена: х = 6^y. x₁ = 6¹ =6. x^(-2) = 1/36.Так как переменная в знаменателе, то меняем знак неравенства, кроме того, учитываем х ≠ 216.Область решений заданного неравенства разбивается на 3 промежутка:0 < x ≤ (1/36), 6 ≤ x < 216, x > 216.
-
Автор:
madeleine4pv4 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Радиоактивный атом 238 91Pa получил а- и ß- распад. Какое ядро появилось в ходе этого превращения? Запишите реакции
-
Из одного пункта одновременно вышли два лыжника и отправились в противоположных направлениях. Скорость первого лыжника равна 12 км/ч, а второго - 15 км/ч. Через некоторое время они остановились. В тот момент расстояние между ними было равно 81 км. Сколько времени они были в пути остановки?
-
Предмет:
Математика -
Автор:
livia - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Подобрать проверочные слова:посадить,словесный,окончательно,выбросить,подарить,продавец,уплотнение,водительский,ходьба,долина,разъединять,приближались,пожалеть
-
Предмет:
Русский язык -
Автор:
punk77 - 5 лет назад
-
Ответов:
4 -
Смотреть
-
-
Какие есть формальные языки и для чего они предназначены?
-
Предмет:
Информатика -
Автор:
jerónimo - 5 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
