Задать вопрос Регистрация
Помочь другим

  • Найти общее решение данного уравнения и частное решение, удовлетворяющее данным начальным условиям.

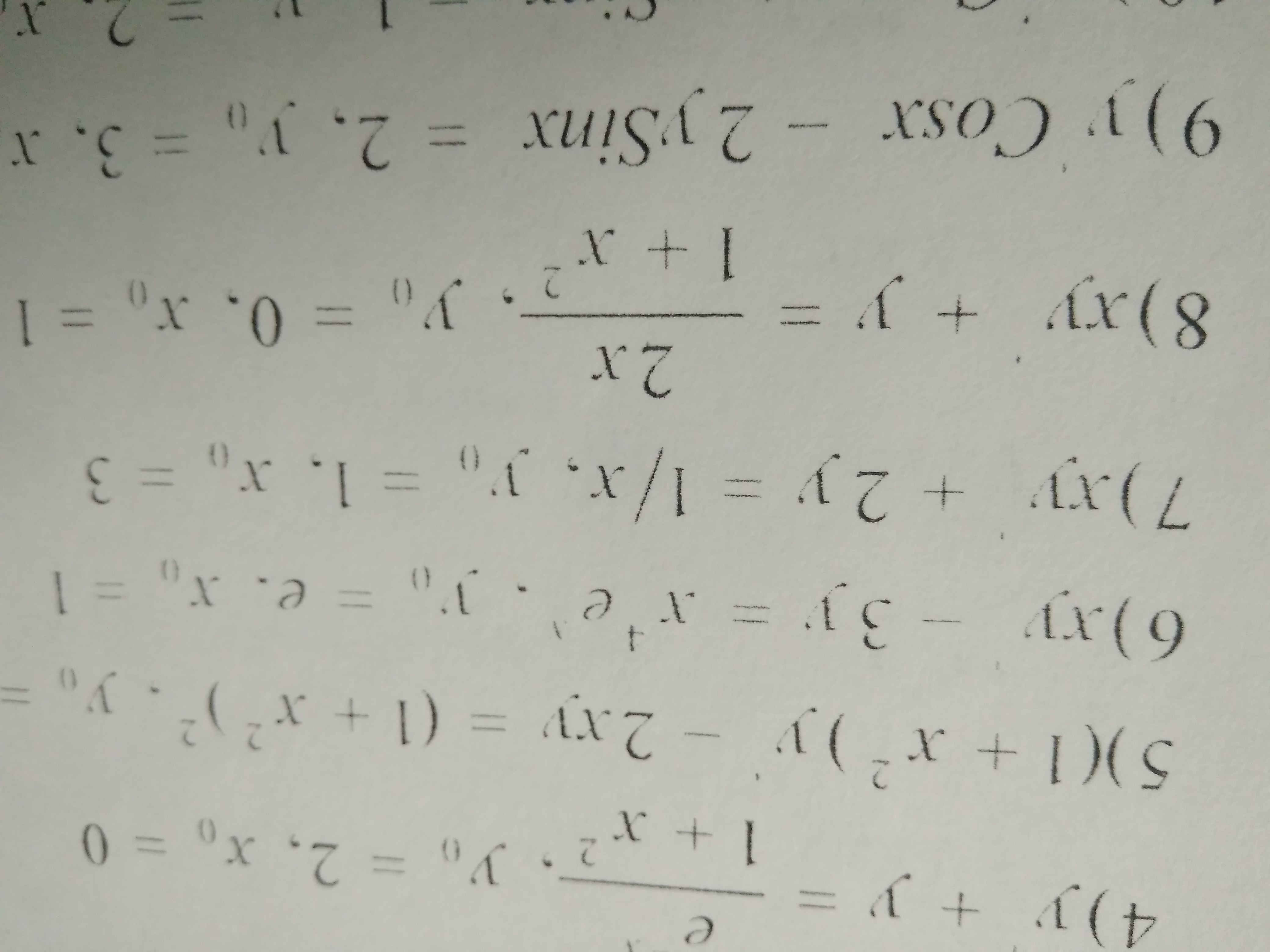
    question img

Ответы 1

  • 7)xy'+2y= \frac{1}{x} y'+ \frac{2y}{x} = \frac{1}{x^2} y=uvu'v+uv'+ \frac{2uv}{x} = \frac{1}{x^2}u'v+u(v'+ \frac{2v}{x} )= \frac{1}{x^2}v'+ \frac{2v}{x}=0 \frac{dv}{dx}=- \frac{2v}{x} \frac{dv}{dx}=- \frac{2v}{x}\int \frac{dv}{v}=-2\int \frac{dx}{x}ln |v| =-2ln|x|ln |v| =ln| \frac{1}{x^2} |v=\frac{1}{x^2}u'v=\frac{1}{x^2}\frac{u'}{x^2}=\frac{1}{x^2}\frac{du}{dx}=1\int du =\int dxu=x+Cy=uv= \frac{x+C}{x^2} y(3)=\frac{3+C}{3^2} =13+C=9C=6y=\frac{x+6}{x^2}

    • Автор:

      amara
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years