-
Найти частное решение дифференциального уравнения и вычислить значение полученной функции y=φ(x) при x=x0 с точностью до двух знаков после запятой.
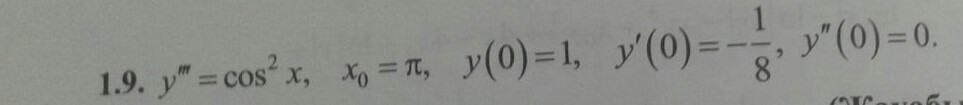
-
Предмет:
Математика -
Автор:
michael35 - 5 лет назад
-
Ответы 1
-
1.9.
Разделяем переменные, интегрированием находим вторую производную. У косинуса понижаем степень, используя формулу двойного угла.
Повторяем интегрирование. Для нахождения постоянной интегрирования используем начальные условия.
Ещё раз повторяем.
Подставляем и считаем
-
Автор:
tyson81 - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
14 слов на букву В пжжжж помогите если хотите еще рдин вопрос пишите #хочувопрос
-
Предмет:
Русский язык -
Автор:
bonifacio - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
у меня есть стол, компьютер, телевизор, шкаф, стулья, кровать, диван, ковер, телефон, лампа как написать по английскаму
-
Предмет:
Английский язык -
Автор:
giovanizh1d - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Помогите написать рассказ на тему Астана
-
Предмет:
Қазақ тiлi -
Автор:
natividad - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
Коля купил 3 ко картофеля по цене 9 р. за килограмм. У него осталось 237 р. Сколько денег было у Коли? Условие, решение и ответ
-
Предмет:
Математика -
Автор:
bullwinkle - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
