Задать вопрос Регистрация
Помочь другим

  • Найти частное решение линейного однородного уравнения

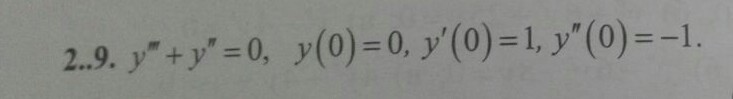
    question img

Ответы 1

  • 2.9. y'''+y''=0Составляем характеристическое уравнение\lambda^3 +\lambda^2 =0 \\ \lambda^2 (\lambda+1) = 0 \\ \\ \lambda_1 = -1 \\ \lambda_{2,3} = 0Решение в виде:y = C_1e^{\lambda_1 x} + C_2 xe^{\lambda_2 x} + C_3e^{\lambda_3 x}y = C_1e^{-x} + C_2 xe^{0} + C_3e^{0} = C_1e^{-x} + C_2 x + C_3 \\ \\ y' = -C_1 e^{-x}+C_2 \\ \\ y'' = C_1 e^{-x} \\ \\ y''(0) = C_1 e^{0} = C_1 = -1 \\ y'(0) = -(-1) e^{0}+C_2 = 1 + C_2 = 1; C_2 = 0 \\ y(0) = -e^{0} + C_2 *0 + C_3 = -1 +C_3= 0; C_3 = 1 \\ \\ y = C_1e^{-x} + C_2 x + C_3 = -e^{-x} +1

    • Автор:

      carney
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years