Задать вопрос Регистрация
Помочь другим

  • дан степенной ряд. Найти интервал сходимости ряда и исследовать его сходимость на концах интервала

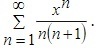
    question img

Ответы 6

  • А вы не поинтересовались, что имели ввиду? Может, ещё хотели сумму ряда найти? Так такого вопроса не было.

    • Автор:

      good71
    • 5 лет назад
    • 0
  • Ну, ещё можно указать радиус сходимости, R=1, но это из интервала сходимости следует само собой...Но и про R вопроса не было.
  • Или надо было подробнее расписать про сходимость на концах интервала? Но за 9 баллов подробности пишите сами. И так всё ясно.

    • Автор:

      josie19
    • 5 лет назад
    • 0
  • А всё-таки "спасибо" не мешало бы отметить ...
  • ой, извеняюсь. Я просто ответ не записал)))

    • Автор:

      brenden
    • 5 лет назад
    • 0
  • \sum\limits _{n=1}^{\infty }\, \frac{x^{n}}{n(n+1)}\\\\ \lim\limits _{n \to \infty}\, \frac{a_{n+1}}{a_{n}}= \lim\limits _{n \to \infty} \frac{|x|^{n+1}}{(n+1)(n+2)}\cdot \frac{n(n+1)}{|x|^{n}}=|x|\ \textless \ 1\\\\-1\ \textless \ x\ \textless \ 1\\\\x=1:\; \; \sum\limits _{n=1}^{\infty } \frac{1}{n(n+1)}\ \textless \ \sum\limits _{n-1}^{\infty }\frac{1}{n^2}\; \; -\; \; sxoditsya\\\\x=-1:\; \; \sum\limits _{n=1}^{\infty } \frac{(-1)^{n}}{n(n+1)}\; \; -\; \; absol.sxod.\\\\oblast\; sxodimosti:\; \; -1 \leq x \leq 1

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years