Найти частное решение дифференциального уравнения удовлетворяющее начальным условиям.

Найти частное решение дифференциального уравнения удовлетворяющее начальным условиям.
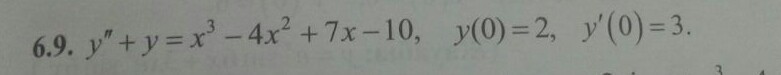
- Предмет:
  Математика
- Автор:
  colt
- 5 лет назад

Ответы 4

Спасибо большоое
- Автор:
  milohenson
- 5 лет назад
- 0
а это задание не решается https://znanija.com/task/27710800
- Автор:
  colton
- 5 лет назад
- 0
Последнее задание))
- Автор:
  amiahqvqk
- 5 лет назад
- 0
6.9. $y''+y=x^3-4x^2+7-10$ Ищем общее решение Y однородного уравнения: $y''+y =0$ Характеристическое уравнение: $\lambda^2+1 = 0 \\ \lambda^2 = -1 \\ \lambda = \pm i$ Имеем два сопряжённых комплексных корня характеристического уравнения: $\lambda_1 = \alpha - \beta x = 0 - 1*i = -i \\ \lambda_2 = \alpha + \beta x = 0 + 1*i = +i$ следовательно, общее решение однородного уравнения имеет вид: $Y = e^{ \alpha x}( C_1 cos \beta x + C_2 sin \beta x)$ Подставляем наши значения: $Y = e^{ 0* x}( C_1 cos (1*x) + C_2 sin (1*x)) = C_1 cos x + C_2 sin x$ Т.к. правая часть содержит степенную функцию, то частное решение ищем в виде: $y = Ax^3+Bx^2+Cx+D \\ \\ y' = 3Ax^2+2Bx+C \\ \\ y'' = 6Ax + 2B$ Используем метод неизвестных коэффициентов, чтобы найти наши A, B, C, D, для чего предполагаемую функцию и её вторую производную подставляем в исходное уравнение: $6Ax + 2B + Ax^3 + Bx^2 + Cx + D = x^3-4x^2+7-10 \\ \\ Ax^3 +Bx^2 + (6A+C)x + (2B+D) = x^3-4x^2+7-10 \\ \\ \\ A = 1 \\ B= -4 \\ 6A+C = 7; C=7-6*1= 1 \\ 2B+D = -10; D = -10 -2*(-4) = -2$ Итак, частное решение такое: $y = x^3-4x+x-2$ Суммируем общее и частное решения Y + y: $y = C_1 cos x + C_2 sin x + x^3-4x^2+x-2$ Находим частное решение по начальным условиям:y(0) = 2; y'(0) = 3Находим производную: $y' = (C_1 cos x + C_2 sin x + x^3-4x^2+x-2)' = \\ \\ =-C_1 sinx + C_2 cosx +3x^2 -8x +1$ Подставляем начальные значения в у и у' $y(0) = C_1 cos 0 + C_2 sin 0 + 0^3-4*0^2+0-2 = C_1 - 2 =2; C_1= 4 \\ \\ y'(0) = -C_1 sin0 + C_2 cos0 +3*0^2 -8*0 +1 =C_2 +1 =3; C_2= 2$ Благодаря начальным условиям нашли неизвестные коэффициенты $C_1, C_2$ , а требуемое решение выглядит так: $y = 4 cos x + 2sin x + x^3-4x^2+x-2$
- Автор:
  maestro
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Ответы 4

Топ пользователей