-
Нужен ответ с решением и объяснением. Буду очень благодарен)
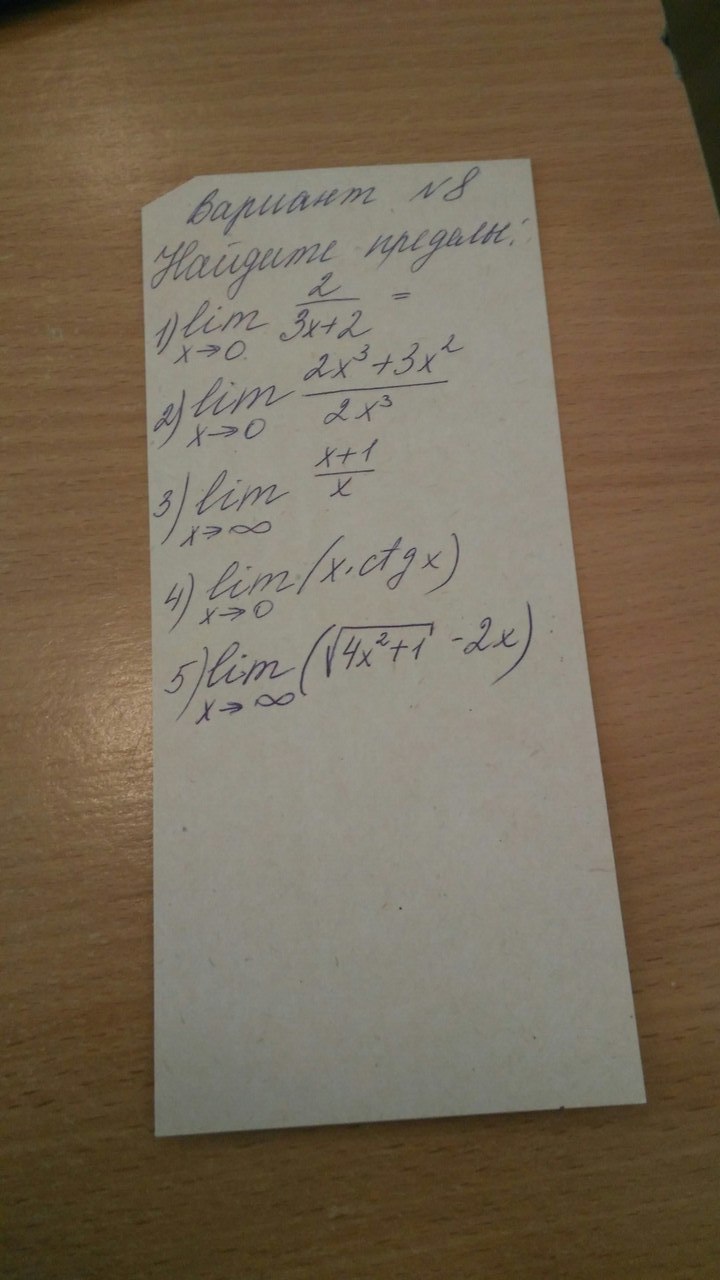
-
Предмет:
Математика -
Автор:
buffalousnd - 5 лет назад
-
Ответы 2
-
Можешь еще кое с чем помочь?
-
Автор:
tarsiciomzah - 5 лет назад
-
0
-
-
Просто подставляем
.
Число поделить на нуль - это бесконечность.
Константой можно пренебречь по сравнению с бесконечностью.
В этом пределе использован первый замечательный предел:
Опять пренебрегаем константой по сравнению с членом, стремящимся к бесконечности.
-
Автор:
acevedo - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
ПОМОГИТЕ ПОЖАЛУЙСТА. СРОЧНО ОЧЕНЬ
упростить (3х-х^2\x^2-6x+9+2x\2x+5)умножить на (2х^2-x-15)=-
Предмет:
Алгебра -
Автор:
kierradonovan - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Масса кристаллогидрата 7,3 г
Масса воды 3,6 г
Надо найти сколько воды в растворе CaCl2 x XH2O -
что такое атласный ???????????????????
-
Предмет:
Русский язык -
Автор:
camilahughes - 5 лет назад
-
Ответов:
2 -
Смотреть
-
-
Расчёт давления жидкости на дно и стенки сосудов
Помогите плиз
Срочно
How much to ban the user?
1 hour
1 day
100 years
