Середина бічної сторони рівнобедреного трикутника віддалена від його основи на 9 см. Знайдіть відстані від точки перетину медіан трикутника до його основи.

Ответ:

6 см

Пошаговое объяснение:

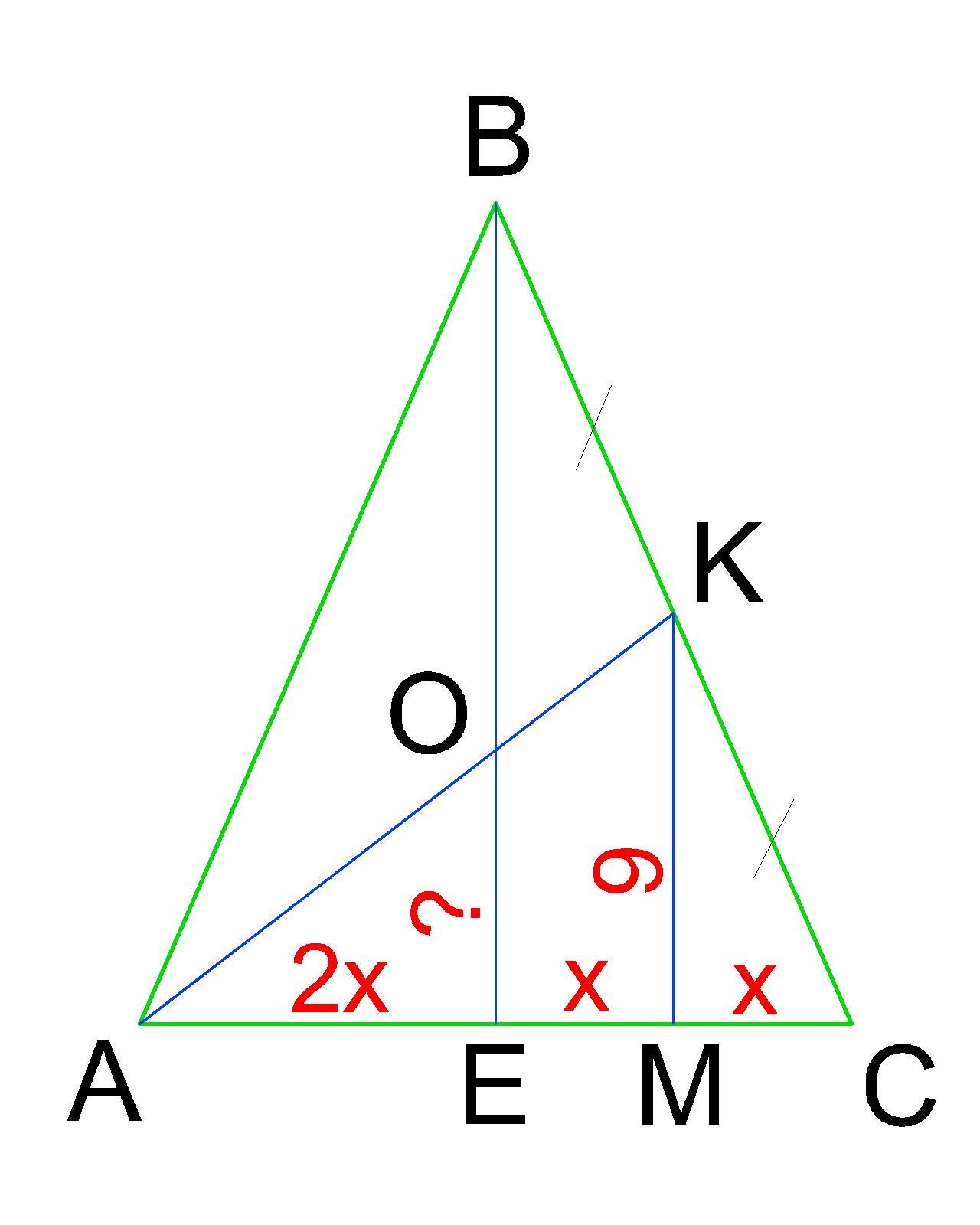
Побудуємо рівнобедрений ΔАВС. Проведемо в ньому медіани ВЕ і АК. Вони перетинаються у точці О. Проведемо висоту КМ = 9 см з середини бічної сторони ВС на основу АС. Треба знайти ОЕ.

КМ║ВЕ, тому що ВЕ⊥АС, як медіана, проведена до основи рівнобедреного трикутника.

Тоді із теореми про паралельні прямі, що перетинають сторони кута, відтинають від сторін кута пропорційні відрізки:

\frac{BK}{KC} =\frac{EM}{MC} =1.

Нехай ЕМ=МС=х, тоді АЕ=2х (т.я. АЕ=ЕС=ЕМ+МС).

Розглянемо ΔАКМ і ΔАОЕ. Вони подібні, так як у них ∠А спільний і ∠ОЕА=∠КМА=90°. Тоді:

\frac{KM}{OE} =\frac{AM}{AE} \\\frac{9}{OE} =\frac{AE+EM}{AE} \\\frac{9}{OE} =\frac{3x}{2x} \\OE=\frac{9*2}{3} =6