Найти общее решение линейного неоднородного дифференциального уравнения второго - Дата: 20.01.2020, Автор: jared

Найти общее решение линейного неоднородного дифференциального уравнения второго порядка.
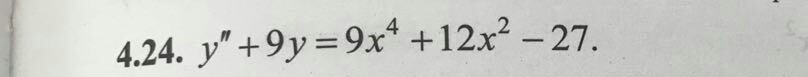
- Предмет:
  Математика
- Автор:
  jared
- 5 лет назад

Ответы 1

4.24. $y'' +9y = 9x^4 + 12x^2 -27$ Имеем линейное неоднородное уравнение второго порядка. Решаем сначала однородное уравнение: $y'' +9y = 0$ .Как обычно, составляем характеристическое уравнение и решаем его. $\lambda^2 + 9 = 0 \\ \\ \lambda = \pm 3i$ Характеристическое уравнение имеет два чисто мнимых корня: $\lambda_1 = 0 + 3 i \\ \lambda_2 = 0 - 3 i$ Поэтому общее решение: $y = e^{ \alpha x}(C_1 cos \beta x + C_2 sin \beta x)$ упрощается, т.к. у нас: $\alpha =0; \: \beta =3$ И будет иметь вид: $y = C_1 cos \beta x + C_2 sin \beta x$ Подставляем своё значение: $y = C_1 cos 3x + C_2 sin 3x$ Теперь надо найти частное решение. Т.к. в правой части у нас многочлен 4-й степени, то решение и ищем в таком виде: $\widetilde{y} = Ax^4 +Bx^3 +Cx^2 +Dx + E$ Найдём вторую производную, а затем её и саму функции подставим в исходное уравнение: $\widetilde{y'} = 4Ax^3 +3Bx^2 +2Cx + D \\ \\ \widetilde{y''} = 12Ax^2 +6Bx +2C \\ \\ 12Ax^2 +6Bx +2C + 9(Ax^4 +Bx^3 +Cx^2 +Dx + E) = \\ \\ = 9x^4 + 12x^2 - 27$ $9Ax^4 +9Bx^3+ (12A+9C)x^2 +(6B+9D)x +(2C + 9E) = \\ \\ = 9x^4 + 12x^2 - 27 \\ \\ A=1; \: B=0; \: 12A + 9C = 12; \: 6B + 9D =0; \: 2C + 9E = -27 \\ \\ 12*1 +9C = 12 \Rightarrow C = 0 \\ \\ 6*0 +9D = 0 \Rightarrow D = 0 \\ \\ 2*0 + 9E = -27 \Rightarrow E = -3 \\ \\ \widetilde{y} = 1*x^4 +0*x^3 +0*x^2 +0*x - 3 \\ \\ \widetilde{y} =x^4 - 3$ Объединяем решения: $y = y + \widetilde{y} \\ \\ y = C_1 cos \beta x + C_2 sin \beta x + x^4 - 3$
- Автор:
  tyson40
- 5 лет назад
- 0
Добавить свой ответ