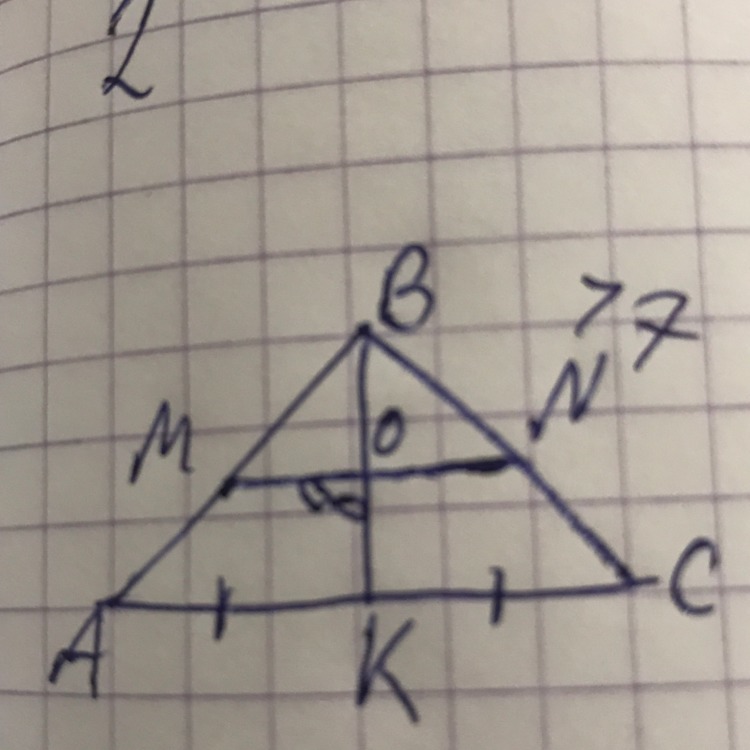
В равнобедренном треугольнике ABC с основа- нием AC медиана BK =8, боковая сторона BC = 17 . Найдите отрезок MN , если известно, что он соединяет середины боковых сторон.

Так как по условию АВС - равнобедренный и MN соединяет середины боковых сторон, то MN является средней линией треугольника АВС.Мы помним, что средняя линия равна половине основания. В данном случае половине АС.  Так как ВК медиана по условию, это значит что  АК=КС.Теперь нам достаточно узнать КС - ведь это половина основания АС.Рассмотрим треугольник КВС. Он прямоугольный, так как ВК является медианой, и высотой в равнобедренном треугольнике. Угол ВКС=90 градусов, он прямой.Применим т.Пифагора:ВС в квадрате=ВК в квадрате + КС в квадратеНайдем КС в квадрате=17*17-8*8КС в квадрате =289-64=225КС= корень из 225КС=15Еще раз повторю MN -это средняя линия, и она равна половине основания АС, а КС и есть половина основания. Значит, MN=15Ответ: MN=15