-
помогите пожалуйста уже запарился с этой темой даже к репетитору ходил за деньги ни хрена не понял объясните пожалуйста и решите
2)
4)
6)
уже закалибался с этой темой даю 100 балов только объясните пж! А то ещё завтра контрольная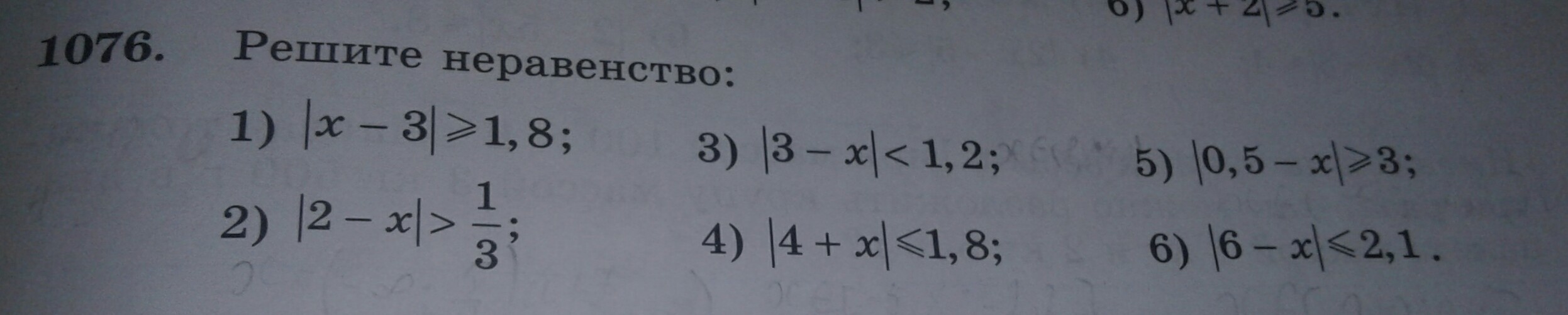
-
Предмет:
Математика -
Автор:
keely - 6 лет назад
-
Ответы 6
-
ЗАПУТАЛИИИ
-
Автор:
craigabbott - 6 лет назад
-
0
-
-
ну ок спасибо вам попробую ещё сам разобраться
-
Автор:
hanktp89 - 6 лет назад
-
0
-
-
Подождите, давайте ещё раз попробуем разобраться вместе. Для этого наш сайт и создан. Спрашивайте что именно непонятно. Не бойтесь задавать вопросы.
-
Автор:
ruperto - 6 лет назад
-
0
-
-
хорошо
-
Автор:
champ86 - 6 лет назад
-
0
-
-
спасибо
-
Автор:
harpertbkn - 6 лет назад
-
0
-
-
Алгоритм решения задач с модулем:1) |x|<a -a < x < a2) |x|>a x>a и x<-a1.Если посмотреть на модуль проще, то модуль - это расстояние между числами, стоящими под знаком модуля..2. Расстояние можно откладывать на числовой прямой как влево , так и вправо.2) |2-x| > 1/3 (первый пример разберём подробно) Числа под знаком модуля меняем местами (чтобы на первом месте стоял х (от этого результат не изменится), получаем: |x-2| >1/3 Т.е. расстояние от числа х до числа 2 больше числа 1/3 (Расстояние 1/3 можно отложить от начала отсчёта как вправо , так и влево от начала отсчёта, т.е. при этом мы получим 2 числа 1/3 и -1/3. Если мы откладываем это расстояние 1/3 вправо, то получаем неравенство x-2 > 1/3 Если мы откладываем это расстояние 1/3 влево (при этом получаем число -1/3), то получаем неравенство x-2 < -1/3Графически это выглядит так: /////////////////////// (-1/3)_____________(1/3)///////////////////////////Теперь остаётся решить полученные неравенства и объединить полученные решения:
4) |4+x|≤1,8 -1,8≤ 4+x ≤1,8-1,8-4≤ x ≤1,8-4-5,8 ≤ x ≤ -2,2 x∈[-5,8;-2,2]6) |6-x|≤2,1 |x-6|≤2,1-2,1 ≤ x-6 ≤ 2,1-2,1+6 ≤ x ≤ 2,1+63,9 ≤ x ≤ 8,1x∈[3,9;8,1]
-
Автор:
chaimmoses - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Семь яблок надо поровну разделить между 8 детьми (яблоки одинаковые).<br />
Сколько должен получить каждый ребёнок?-
Предмет:
Математика -
Автор:
evangelineaglu - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
какое утверждение является не правильным ?
а ) У млекопитающих тазовые почки являются органами выделения
б ) Грудина рукокрылых млекопитающих несет киль , к которому прикрепляются грудные мышцы
в ) грудной отдел скелета земноводных несет подвижные ребра соеединены
ененые с грудиной
г ) кожное покрытия ланцетника состоят из эпидермиса и кориума-
Предмет:
Биология -
Автор:
pascualdawson - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Придумайте свою пословицу или поговорку о времени... помогите пожалуйста!!!
-
Предмет:
Обществознание -
Автор:
luke1zbn - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
40 БАЛЛОВ сочинение на тему "Испытание войной" на основе произведения "Журавлиный крик"
-
Предмет:
Литература -
Автор:
natalia20 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
