-
Выразить с помощью формулы двойного угла cos58; sin6pi/7; tg78
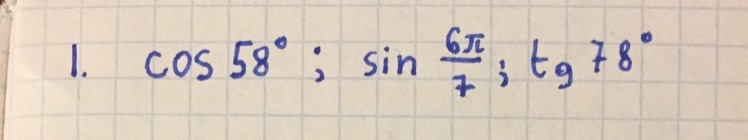
-
Предмет:
Математика -
Автор:
gingerwalton - 6 лет назад
-
Ответы 1
-
Ответ:
\cos \, 58 ^\circ = \cos^2 \dfrac{58^\circ}{2} - \sin^2 \dfrac{58^\circ}{2} = \boxed{ \cos^2 29^\circ - \sin^2 29^\circ }
\sin \, \dfrac{6\,\pi}{7} = 2 \, \sin \, \dfrac{6 \pi}{7 \cdot 2} \, \, \cos \, \dfrac{6 \pi}{7 \cdot 2} = \boxed { 2 \, \sin \, \dfrac{3 \pi}{7} \, \, \cos \, \dfrac{3 \pi}{7} }
\text{tg} \, 78 ^\circ = \dfrac{2 \, \text{tg} \, \dfrac{78^\circ}{2}}{1 - \text{tg}^2 \, \dfrac{78 ^\circ}{2}} = \boxed { \dfrac{2 \, \text{tg} \, 39^\circ}{1 - \text{tg}^2 \, 39^\circ} }
Примечание:
Формулы синуса, косинуса, тангенса и котангенса двойного угла:
- \sin 2 \alpha = 2 \, \sin \alpha \, \cos \alpha
- \cos \, 2\alpha = \cos^2 \, \alpha - \sin^2 \, \alpha
- \text{tg} \, 2\alpha = \dfrac{2 \, \text{tg} \, \alpha}{1 - \text{tg}^2 \, \alpha}
- \text{ctg} \, 2\alpha = \dfrac{\text{ctg}^2 \, \alpha - 1}{2 \, \text{ctg} \, \alpha}
-
Автор:
esiquiofox - 2 года назад
-
2
-
Добавить свой ответ
Еще вопросы
-
Даны 2 целых числа AиВ написать программу выводящую на экран значения квадрата целых чисел от А до В включительно
-
Предмет:
Информатика -
Автор:
piggybu0t - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
14550□ 11855 > < = помогите
-
Предмет:
Математика -
Автор:
sánchez18 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
сравни написание слов, найди девять графических ошибок. телефон телефон
-
Предмет:
Русский язык -
Автор:
victoriatownsend - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сочинение по вопросам Бунина Кавказ. 1) Каким настроении проникнут Кавказ. 2)В чем счастье и несчастье героев? 3)Виноват кто нибудь из героев разыгравшейся трагедии.
-
Предмет:
Литература -
Автор:
butterball - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
