-
Даю 30 баллов: Найти производную данных функций:
1. y= квадратный корень из arcctg(x/2)
2. y= ln квадратный корень (1+x^2)/(1-x^2)
3. y= ln x^ (1/x)
Данные функции представлены на фото ниже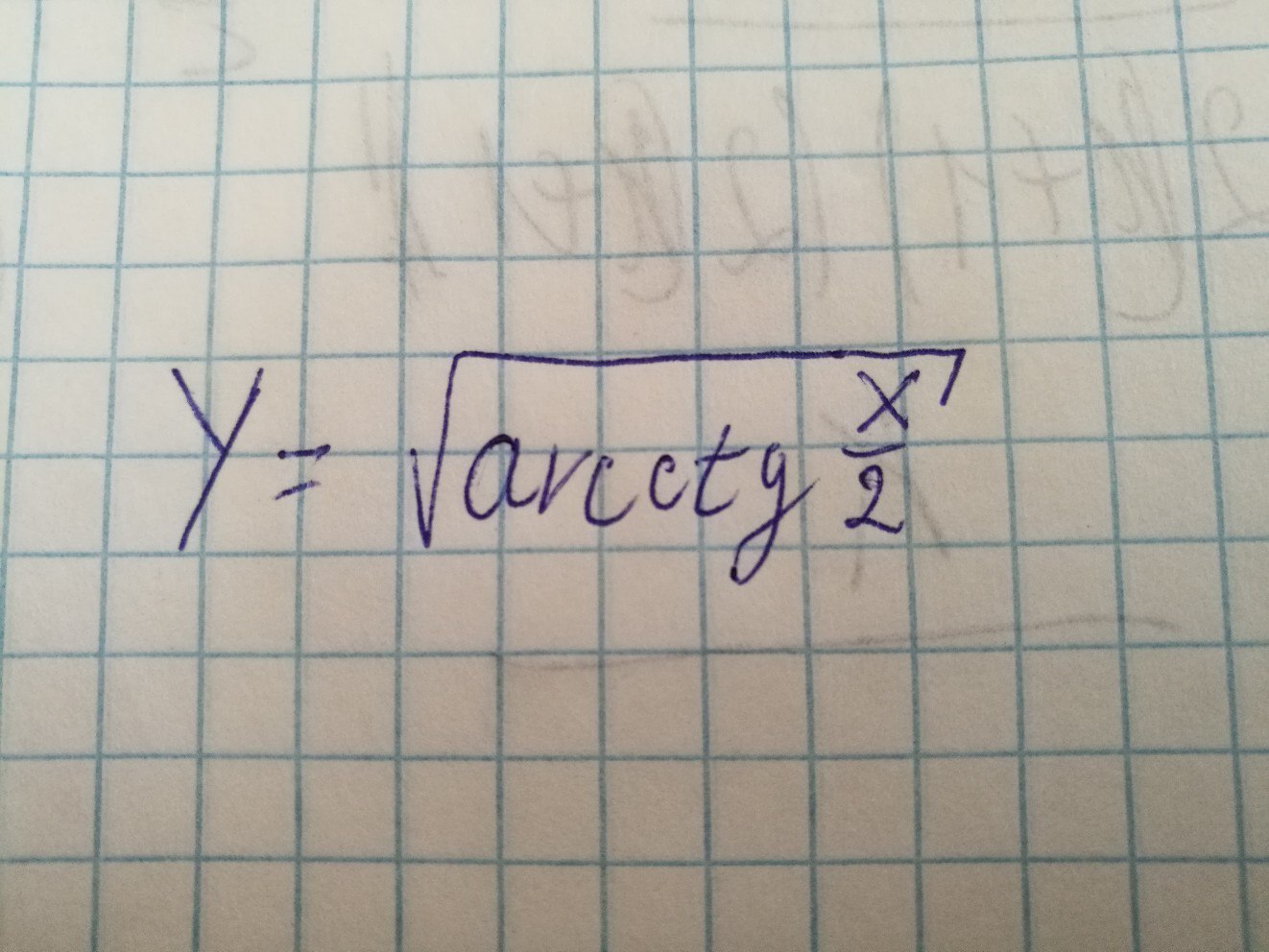
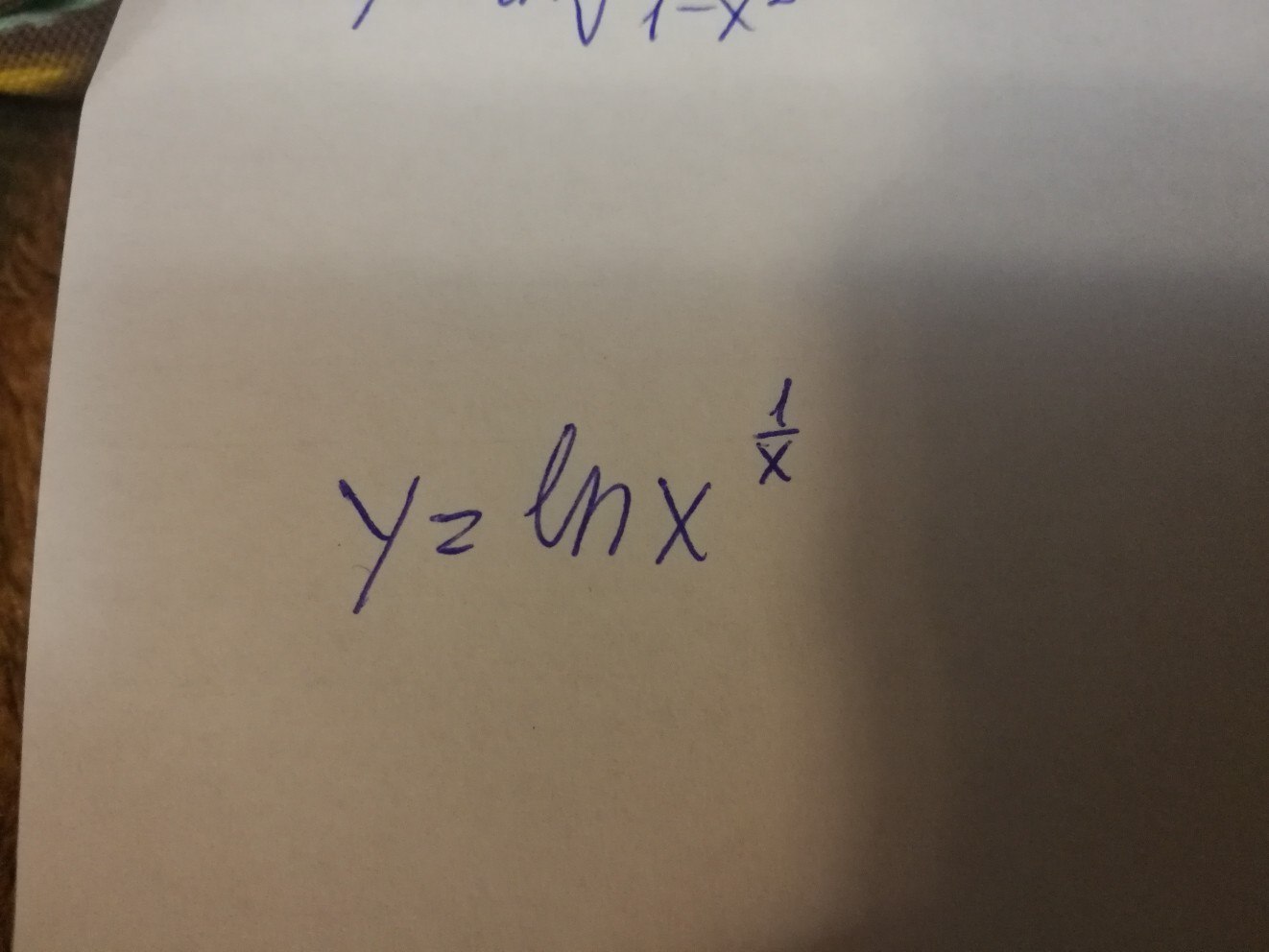
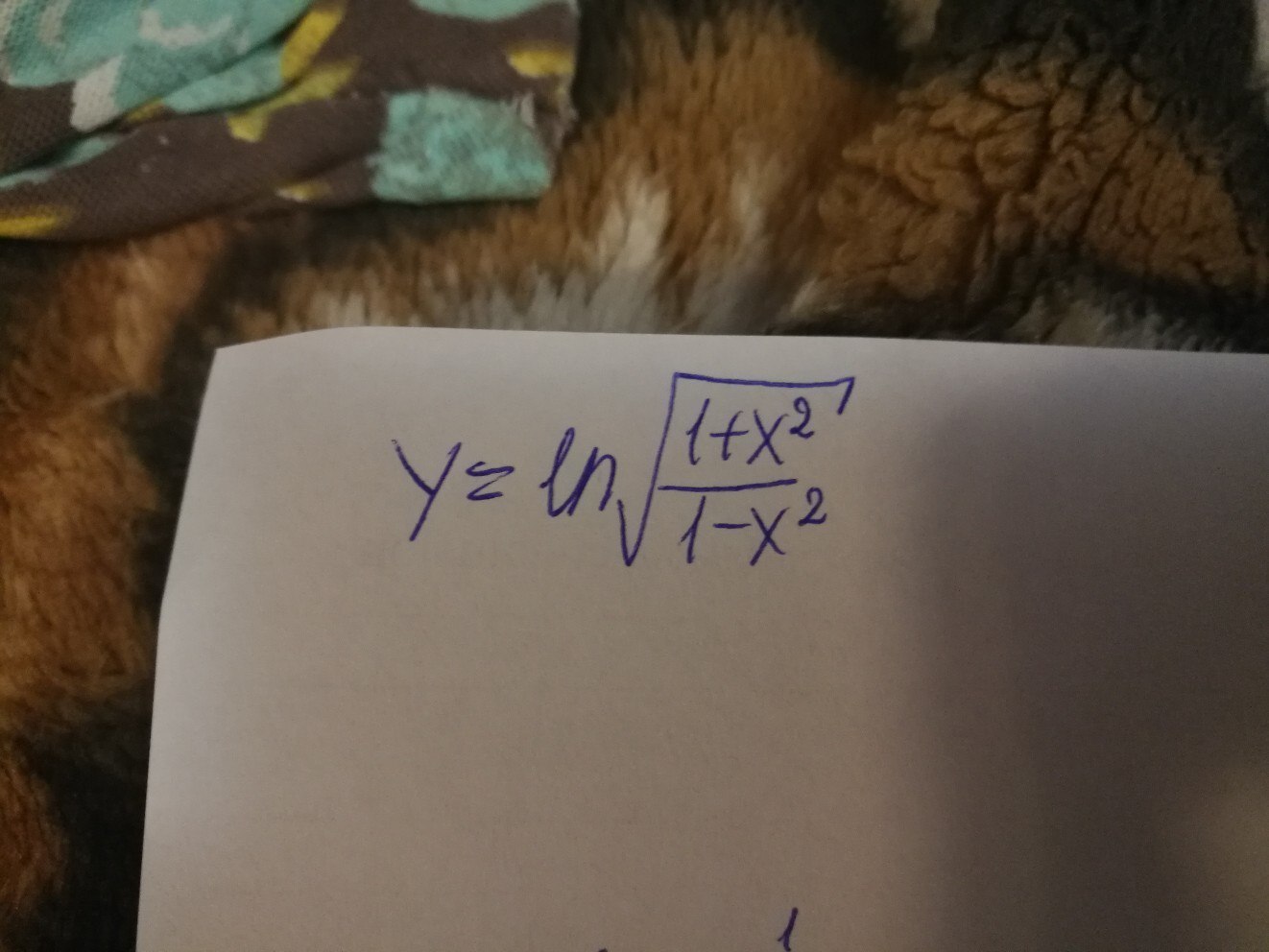
-
Предмет:
Математика -
Автор:
johnathonkoch - 6 лет назад
-
Ответы 1
-
2)
3)
-
Автор:
gonzálezyv5o - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найдите значение числа (1110010111)2 в шестнадцатеричной и восьмеричной системе счисления.
-
Предмет:
Информатика -
Автор:
ducky6nio - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
помогите решить неравенство (x-0,5)*(x+1,3)=0
(*- это умножение)-
Предмет:
Математика -
Автор:
kelvin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Написать реакции
Na2S -- ( Что то вставить) -- SO2 -- SO3 -- H2SO4-
Предмет:
Химия -
Автор:
nickolasmanning - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Составь рассказ от имени путешественника посетившего древние пирей и Афины Включите в рассказ описание морских гаваней длинных стен керамика агоры акрополя.
СРОЧНО!!!
How much to ban the user?
1 hour
1 day
100 years
