-
СРОЧНО!!!! ПОМОГИТЕ ПОЖАЛУЙСТА!!!!
ЖЕЛАТЕЛЬНО РЕШИТЬ ВСЕ!!
Вариант 1
1. На рисунке 165 AB II CD. а) Докажите , что AO:OC=BO:OD. б) Найдите AB , если OD=15 см, OB=9 см, CD=25 см.
2. Найдите отношение площадей треугольников ABC и KMN , если AB=8 см, BC=12 см, AC=16 см, KM=10 см , MN=15 см, NK=20 см.
Вариант 2
1. На рисунке 166 MN II AC. а) Докажите, что AB*BN=CB*BM. б) Найдите MN, если AM=6 см, BM=8 см, AC=21 см.
2. Даны стороны треугольников PQR и ABC: PQ=16 см , QR=20 см, PR=28 см, AB=12 см, BC=15 см, AC=21 см. Найдите отношение площадей этих треугольников.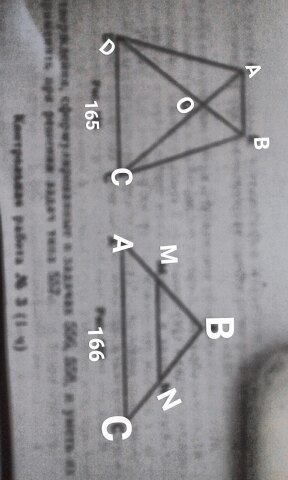
-
Предмет:
Математика -
Автор:
gregory - 6 лет назад
-
Ответы 1
-
1 вариант:1)ΔАОВ подобен ΔСОD,т.к. угол AOB= углуCOD- так как вертикальные; угол BAO= углу DCO и угол ABO= углу CDO - как накрестлежащие, тогда AO:OC=BO:OD (исходя из подобия треугольников)2)ΔАВС подобен Δ KMN, тогда по коэффициенту подобия: k = AB/KM = BC/MN = AC/NK = 8/10 но это число можно сократить, то есть k=8/10=4/5Площади подобных фигур относятся,как квадрат коэффициента подобия:S(ΔABC)/ S(ΔKMN) = k^2=(4/5)^2= 16/25Отве:т 16/252 вариант:1) ΔАВС подобен Δ MBN - по двум углам(угол В- общий, угол ВМN = углу ВАС- как соответственные при МN//АС и секущей АВ)Треугольники подобны, значит сходственные стороны пропорциональны, то есть: АВ/ВМ=СВ/ВN, следовательно AB•BN = СВ•ВМАВ=АМ+МВ=6+8=14МN/АС= ВМ/АВ; МN/21=8/14, МN=21·8/14=12 Ответ МN=12см2) ΔPQR подобен ΔАВС (стороны их пропорциональны):k=PQ/AB=QR/BC=PR/AC=16/12=20/15=28/21, значит k=4/3S(ΔPQR)/ S(ΔАВС) = k^2=(4/3)²=16/9Отве:т 16/9
-
Автор:
furballzkxl - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
16*a=80
57/x=3
Помогите
-
Предмет:
Математика -
Автор:
dotwjar - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
200Г раствора серной кислоты с массовой долей 2% добавили избыток раствора хлорида бария. Какая масса осадка?
-
Предмет:
Химия -
Автор:
jessiemntq - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
вопросы по бетховену
1) Где и когда родился
2) Где и когда умер
3)У кого учился музыки. На каких инст играл.
4)Где учился в Бонне
5)Когда переехал в Вену и чем занимался
6)Знакомые и друзья
7)Где бывал с гастролями
8)Почему бетховена называли венским класиком.
9) Известные произведения
10)Пьеса для фортепиано к Элизе-
Предмет:
Музыка -
Автор:
rigobertoblair - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Могло ли такое быть? Найдите одно неверное утверждение и отметьте его знаком<<->> .
1)У Ивана Третьего была богатая библиотека рукописных книг.
2) В сокровищнице Ивана Третьего хранилась шапка Мономаха
3) К пристаням Москвы-реки причаливали большие морские суда-каравеллы из Португалии и Испании
4)Из сочинений иностранных авторов о Москве времён Ивана Третьего мы узнали много интересного
5) В Москву за товарами приезжали купцы из других русских городов.-
Предмет:
Окружающий мир -
Автор:
acedk2l - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
