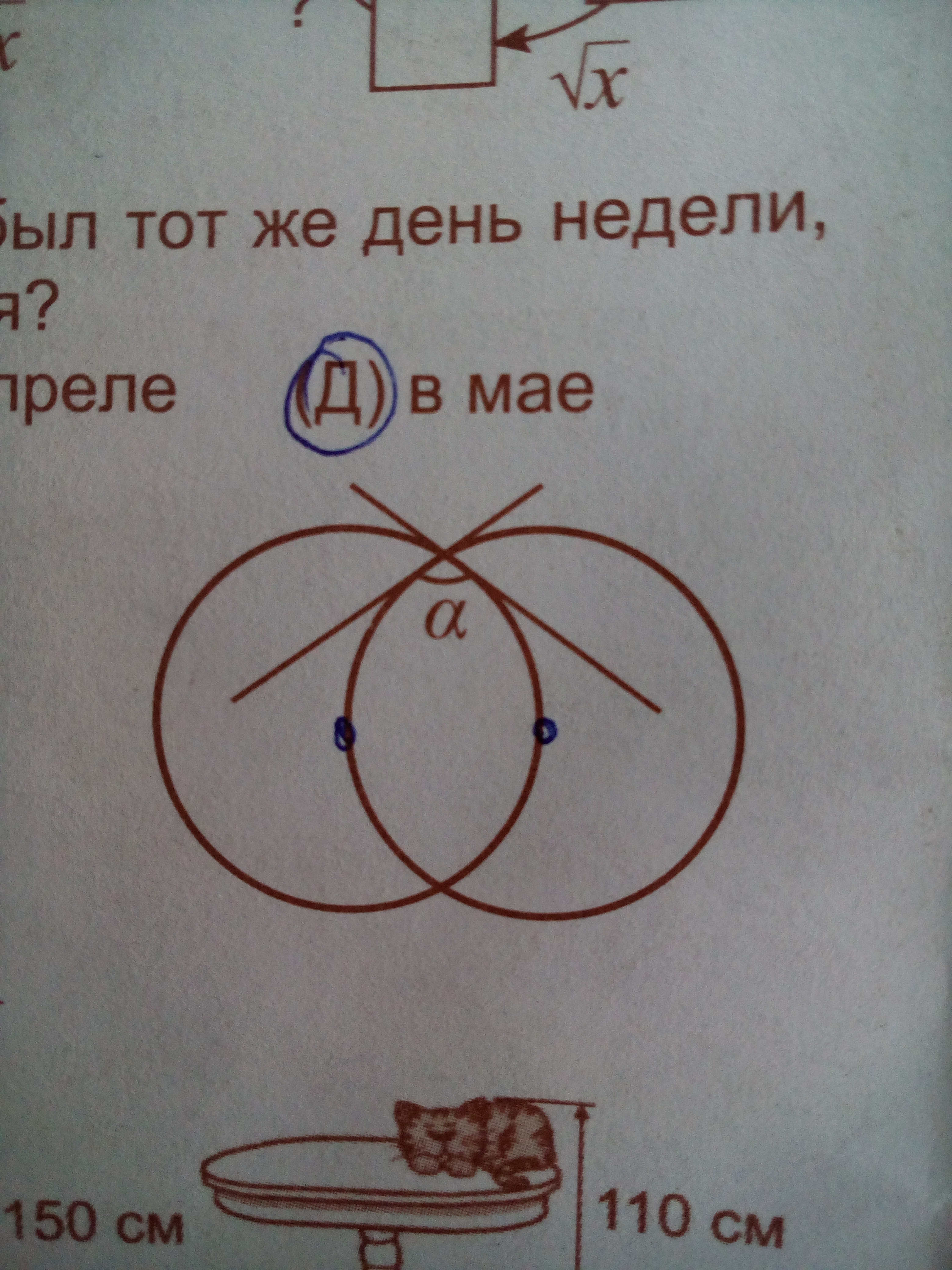
Окружности на рисунке имеют одинаковый радиус и проходят через центры друг друга. В точке пересечения к ним провели касательные. Чему равен угол а?

Соединим центры окружностей их общим радиусом. Также соединим центры окружностей с точкой касания радиусами. Образовался равносторонний треугольник АВС. Радиус АС, проведенный в точку касания, перпендикулярен касательной CD. Значит, угол АСD - прямой. Учитывая, что угол АСВ - угол равностороннего треугольника, равный 60°, получим, что угол ВСD равен 30°. Аналогично, получим, что угол АСЕ равен 30°. Тогда искомый угол α равен сумме углов АСЕ, АСВ и ВСD: α=30°+60°+30°=120° Ответ: 120°