-
Какую операцию нужно добавить,чтобы схему на рисунке можно было правильно заполнить числами,поставив в закрашенную клетку любое положительное число?
А-√x³
Б-³√x²
В-√x
Г-x³
Д-³√x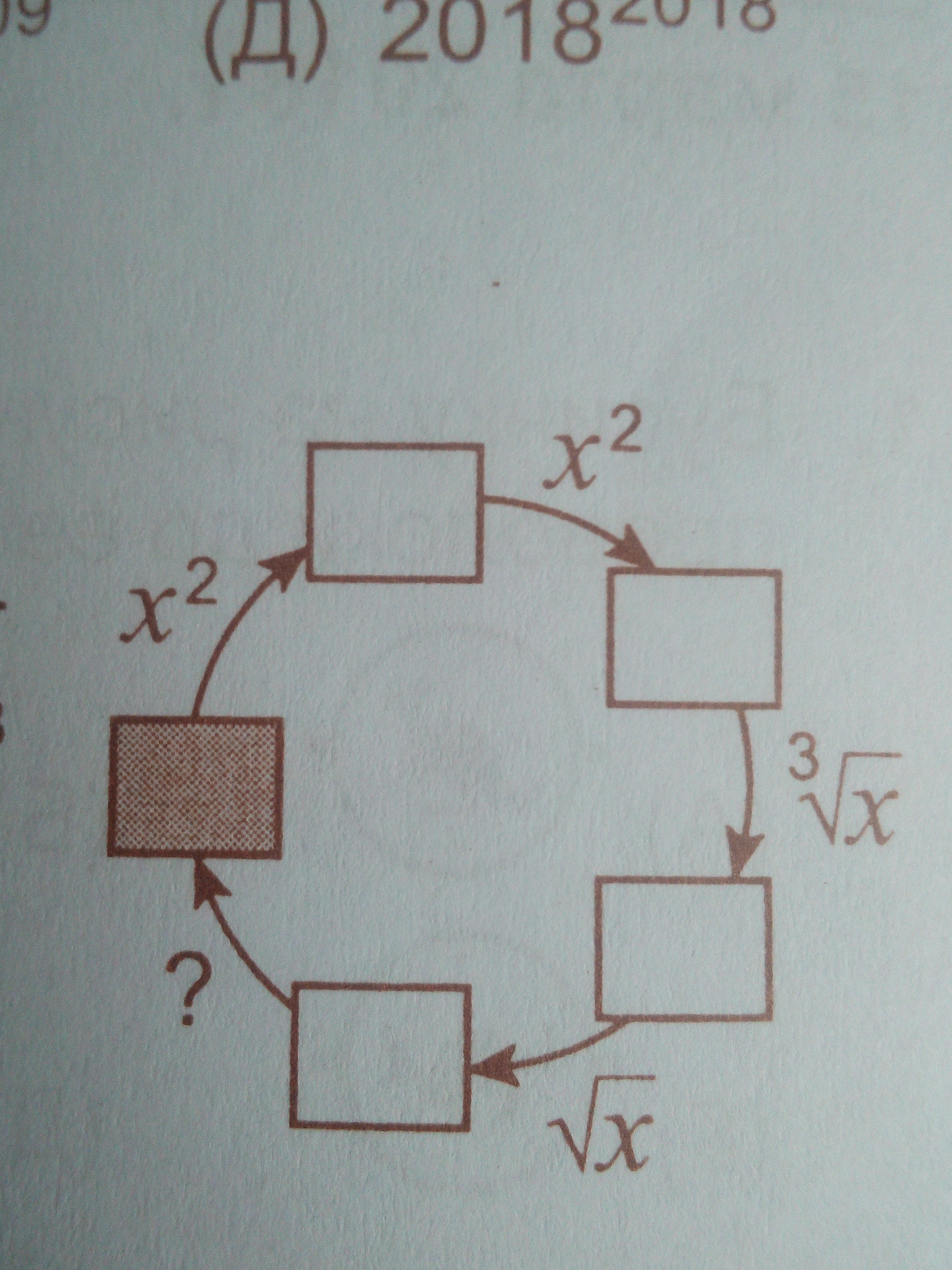
-
Предмет:
Математика -
Автор:
aubriebxhz - 6 лет назад
-
Ответы 1
-
После проведения всех действий мы должны получить исходное число:x\to x^2 \to (x^2)^2 \to \sqrt[3]{(x^2)^2} \to \sqrt{ \sqrt[3]{(x^2)^2} } \to \boxed{x} \sqrt{ \sqrt[3]{(x^2)^2} } =\left( \left(\left(x^2\right)^2\right)^\frac{1}{3} \right)^\frac{1}{2} =x^{2\cdot2\cdot\frac{1}{3}\cdot\frac{1}{2}}=x^{\frac{2}{3}}Найдем в какую степень нужно возвести это выражение, чтобы получить исходное:\left(x^{\frac{2}{3}}\right)^n=x \\\ x^{\frac{2}{3}n}=x \\\ \frac{2}{3}n=1 \\\ n= \frac{3}{2} Таким образом, последняя операция возведение в степень 3/2, то есть применение операции \sqrt{x^3} Ответ: \sqrt{x^3}
-
Автор:
jaceyboyle - 2 года назад
-
19
-
-
Добавить свой ответ
Еще вопросы
-
Помогите пожалуйста надо окончания добавить завтра здавать вот
-
Предмет:
Русский язык -
Автор:
treyll6n - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
ПОМОГИТЕ 30 БАЛЛОВ !!!
УПРАЖНЕНИЕ 121-
Предмет:
Русский язык -
Автор:
jamarcuscantu - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Какое значение имеет спинно-мозговая жидкость??
-
Аліса записала правильну рівність, а потім зафарбувала дві цифри у цій рівності 3-2 =25
-
Предмет:
Математика -
Автор:
admiral82 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
