Задать вопрос Регистрация
Помочь другим

  • Найдите значение производной функции y=f(x) в точке x0 срочно а б в !!!!!!!!

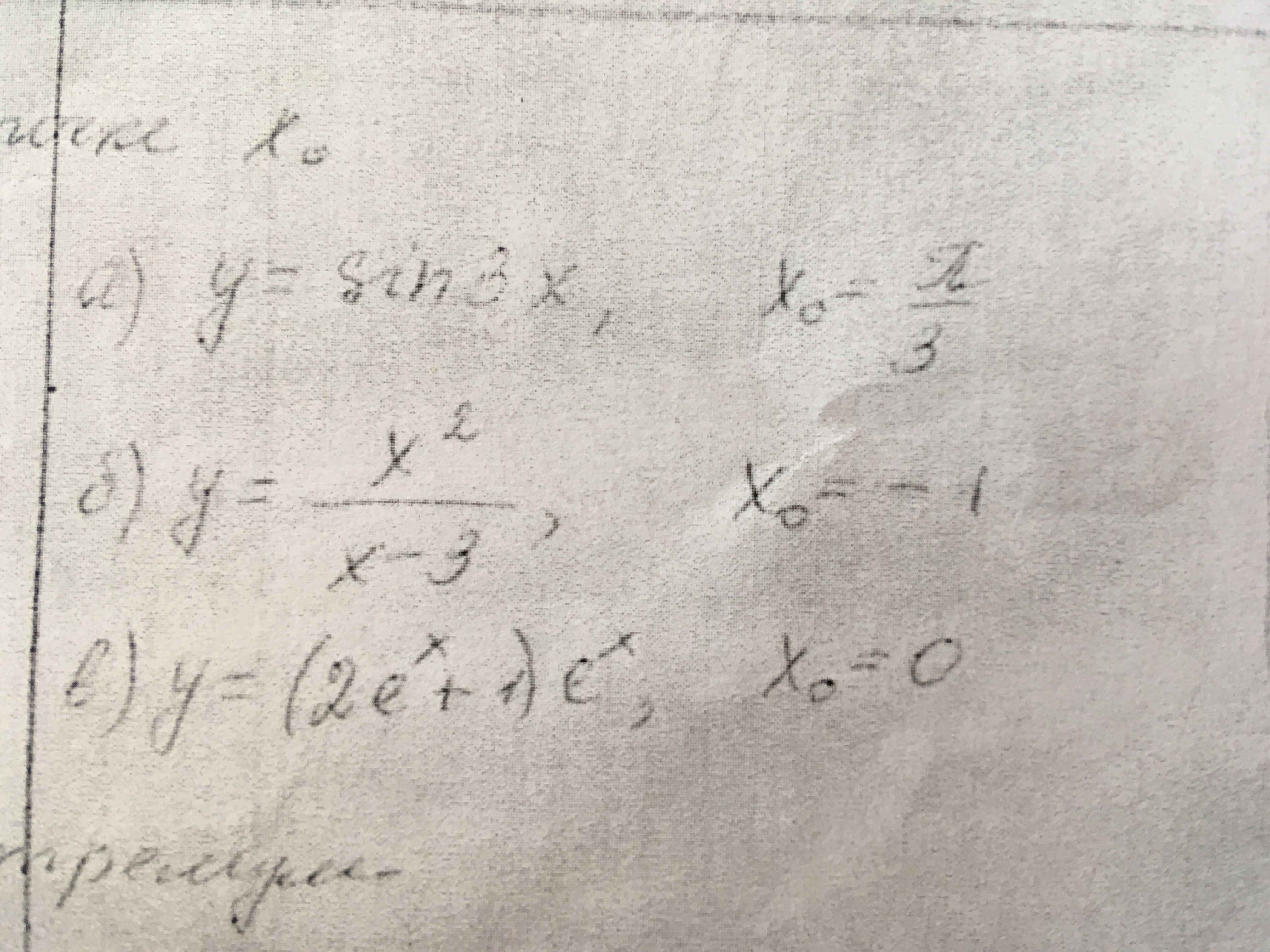
    question img

Ответы 1

  • y=sin(3x)y'=(sin(3x))'=3cos(3x)y'(π/3)=3cos(3*π/3)=3cosπ=3y= \frac{x^2}{x-3} ; \\ y'=( \frac{x^2}{x-3})'= \frac{(x^2)'*(x-3)-x^2*(x-3)'}{(x-3)^2}= \frac{2x(x-3)-x^2}{(x-3)^2} = \frac{2x^2-6x-x^2}{(x-3)^2} = \frac{x(x-6)}{(x-3)^2} \\ y'(-1)= \frac{-1*(-1-6)}{(-1-3)^2} = \frac{7}{16} y=(2e^x+1)*e^x \\ y'=(2e^x+1)'*e^x +(2e^x+1)*(e^x)' = \\ =2e^x*e^x+(2e^x+1)*e^x=2e^{2x}+2e^{2x}+e^x=4e^{2x}+e^xy'(0)=4e^{2*0}+e^0=4+1=5

    • Автор:

      wrinkles
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years