-
Вычислить площадь фигуры, ограниченной линиями. Сделать чертёж
y= 4-(x+2)^2
y=4-4(x-4)^2
y=4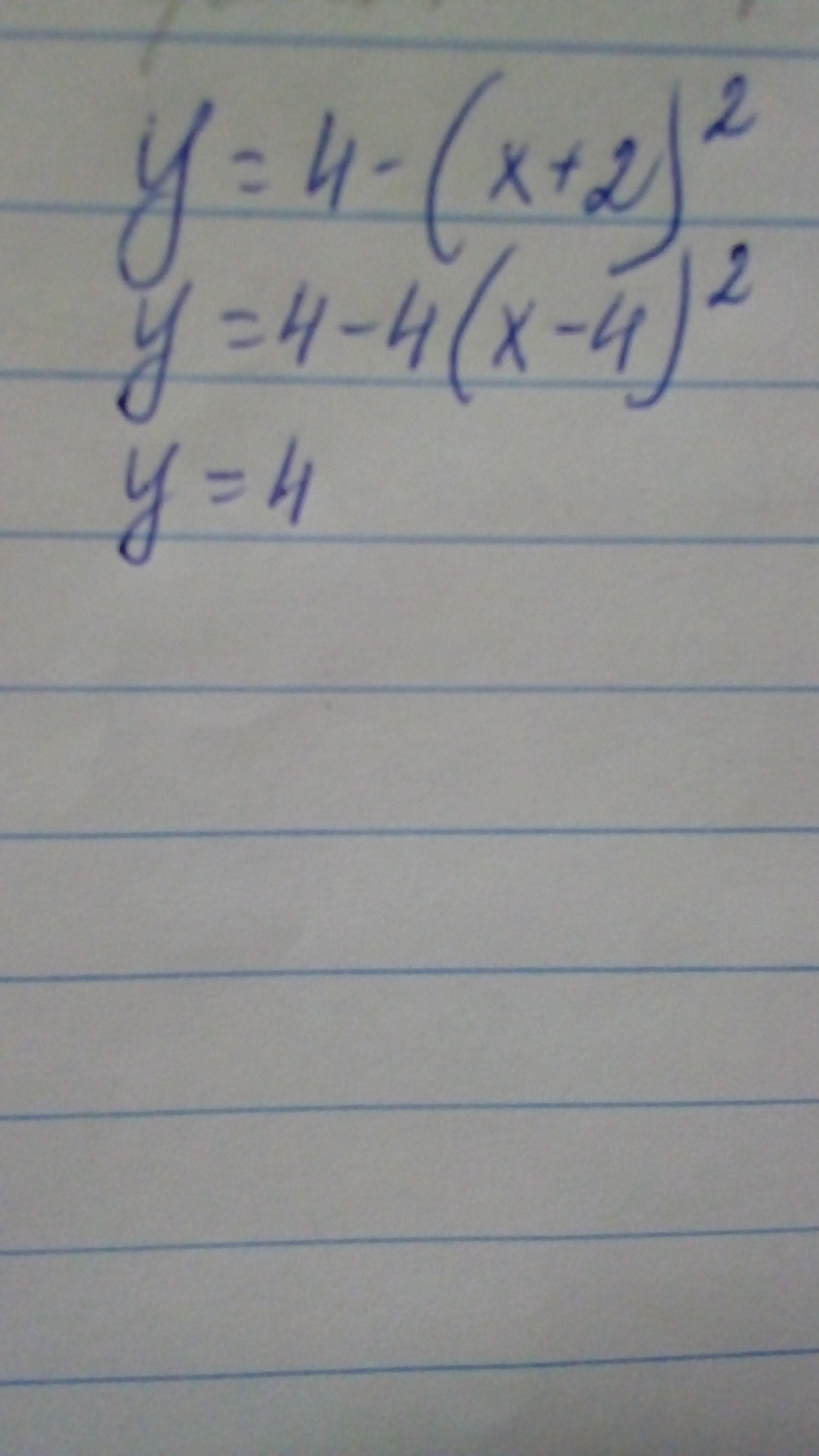
-
Предмет:
Математика -
Автор:
antoniocoleman - 6 лет назад
-
Ответы 1
-
Найдём точки пересечения парабол y=4-(x+2)² и y=4-4(x-4)² .4-(х+2)²=4-4(х-4)² (х+2)²-4(х-4)²=0По формуле А²-В²=(А-В)(А+В) имеем: ((х+2)-2(х-4))·((х+2)+2(х-4))=0 ,(х+2-2х+8)(х+2+2х-8)=0 , (-х+10)(3х-6)=0 ⇒ х=10 и х=2 .Для заданной области подходит х=2 , у(2)=-12 .Точки пересечения с ОХ: 4-(х+2)²=0 ⇒ (2-х-2)(2+х+2)=0 , х=0 и х=-4 .4-4(х-4)²=0 ⇒ (2-2(х-4))·(2+2(х-4))=0 , (10-2х)(2х-6)=0 , х=5 и х=3 .Заданную область разобьём на сумму двух областей прямой х=2 . 1 область: -2≤x≤2 и верхняя граница у₁=4, нижняя граница у₂=4-(х+2)².2 область: 2≤х≤4 и верхн. граница у₁=4, нижняя у₂=4-4(х-4)².Для вычисления площади каждой области пользуемся формулой

-
Автор:
sullivan49 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Расставить знаки препинания и сделать синтаксический разбор предложения: Дом царевна обошла всё порядком убрала.
-
Предмет:
Русский язык -
Автор:
jettwidj - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
1,5(-2,4a+3.8b)-1,6(2,5a-b). Если а= 2, b=-3
-
Предмет:
Математика -
Автор:
brendaxsqs - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Запиши своё имя в разных вариантах. Кто и в каких ситуациях так тебя называет, какой из вариантов имени тебе нравится больше всего? Напиши памятку для своих родных и друзей, чтобы они знали, как именно к тебе лучше обращаться в разных ситуациях. (меня зовут Настя)
-
Предмет:
Русский язык -
Автор:
gabrielaiwt2 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Укажите фразеологизм
1)Считать быстро 2)настоящий друг 3)сесть в калошу 4)Сильно кашляет-
Предмет:
Русский язык -
Автор:
snooptxk5 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
