Задать вопрос Регистрация
Помочь другим

  • Исследуйте функцию и построить ее график. Тема дифференциалы и интегралы.

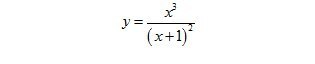
    question img

Ответы 3

  • Пунктирным нужно показать наклонную и вертикальную асимптоту + добавить что-то о горизонтальной асимптоте

    • Автор:

      braun
    • 6 лет назад
    • 0
  • горизонтальная асимптота - частный случай наклонной асимптоты (y=kx+b) при k=0. Отдельным пунктом нет смысла её описывать, так как в данном случае k=1.

    • Автор:

      brett413
    • 6 лет назад
    • 0
  • y = \frac{x^3}{(x+1)^2} 1. Область определения   (x+1)² ≠ 0  ⇒ x≠-1 ⇒  D(y) : (-∞; -1)∪(-1; +∞)2.  \lim_{n \to -1+0} \frac{x^3}{(x+1)^2}=- \infty   ⇒x = -1   Точка бесконечного разрыва   ⇒Вертикальная асимптота    x = -1Наклонные асимптоты  y = kx + bk = \lim_{n \to \infty} \frac{f(x)}{x} = \lim_{n \to \infty} \frac{x^3}{x(x+1)^2} = \\ \\ = \lim_{n \to \infty} \frac{x^2}{(x+1)^2} = \lim_{n \to \infty} \frac{x^2}{x^2+2x+1}= \\ \\ = \lim_{n \to \infty} \frac{ \frac{x^2}{x^2}}{ \frac{x^2}{x^2}+ \frac{2x}{x^2}+ \frac{1}{x^2} }= \lim_{n \to \infty} \frac{1 }{1+ \frac{2}{x}+ \frac{1}{x^2} } \\ \\ k= \frac{1}{1+0+0} =1 b = \lim_{n \to \infty} (f(x)-kx)= \lim_{n \to \infty} (\frac{x^3}{(x+1)^2} -x)= \\ \\ = \lim_{n \to \infty} \frac{x^3-x^3-2x^2-x}{x^2+2x+1} = -\lim_{n \to \infty} \frac{2x^2+x}{x^2+2x+1} = \\ \\ = -\lim_{n \to \infty} \frac{ \frac{2x^2}{x^2}+\frac{x}{x^2} }{ \frac{x^2}{x^2}+ \frac{2x}{x^2} + \frac{1}{x^2} } = -\lim_{n \to \infty} \frac{2+ \frac{1}{x} }{1+ \frac{2}{x} + \frac{1}{x^2} } \\ \\ b= -\frac{2+0}{1+0+0} =-2Одна наклонная асимптота   y = x-23. Нули функцииy = \frac{x^3}{(x+1)^2} =0; x=04. Чётность/нечётностьf(-x)= \frac{(-x)^3}{(-x+1)^2} = -\frac{x^3}{(1-x)^2} Функция общего вида: не является чётной, не является нечётной.Функция не является периодической5. Экстремумы функцииy'= (\frac{x^3}{(x+1)^2} )'= \frac{3x^2(x+1)^2-x^3*2*(x+1)}{(x+1)^4} \\ \\ y'= \frac{x^2(x+1)(3(x+1)-2x)}{(x+1)^4} = \frac{x^2(x+1)(x+3)}{(x+1)^4} \\ \\ y'= \frac{x^2(x+3)}{(x+1)^3} =0x²(x+3) = 0     x₁ = 0;   y₁ = 0/1 = 0x₂ = -3;  y₂ = (-3)³/(-3+1)² = -6,751) x∈(-1;0)  y' >0;       x∈(0; +∞)    y' > 0  ⇒Первая производная знак не меняет ⇒ экстремума в точке нет2) x∈(-∞; -3)    y' >0;       x∈(-3; -1)    y' < 0 ⇒Первая производная в точке x = -3 меняет знак с "+" на "-" ⇒точка  (-3; -6,75) - максимум функции6. x∈(-∞; - 3)  y' > 0     функция возрастает    x∈(-3; -1)   y' < 0     функция убывает    x∈(-1; +∞)  y' > 0    функция возрастает7. Точки перегиба y''= (\frac{x^3+3x^2}{(x+1)^3})' = \frac{(3x^2+6x)(x+1)^3-(x^3+3x^2)*3*(x+1)^2}{(x+1)^6} = \\ \\ = \frac{3(x+1)^2((x^2+2x)(x+1)-(x^3+3x^2))}{(x+1)^6} = \\ \\ = \frac{3(x^3+3x^2+2x-x^3-3x^2)}{(x+1)^4} = \frac{3(2x)}{(x+1)^4} \\ \\ y''= \frac{6x}{(x+1)^4} =0 6x = 0  ⇒   x = 0   -  точка перегибаx∈(-∞; -1)   y'' < 0   график функции выпуклыйx∈(-1;0)      y'' < 0   график функции выпуклыйx∈(0; +∞)    y'' > 0  график функции вогнутый
    answer img

    • Автор:

      ahmed1bxd
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years