-
Изменить порядок интегрирования. Задание прикрепила. Решите плизз❤️ дам 100 баллов)
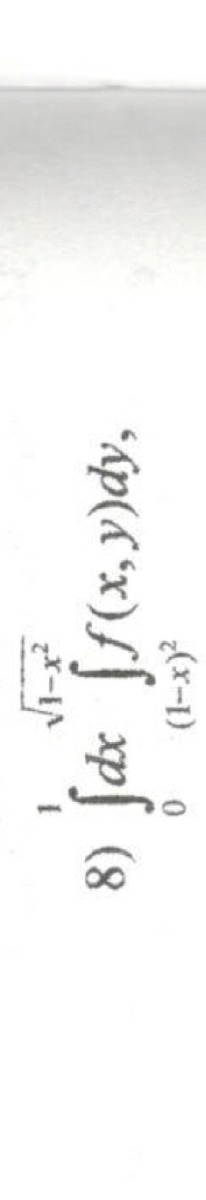
-
Предмет:
Математика -
Автор:
mauricereese - 6 лет назад
-
Ответы 4
-
а не подскажете, как [tex] на наш язык перевести?
-
Автор:
bram3tkc - 6 лет назад
-
0
-
-
просто затрудняюсь последний абзац прочитать
-
Автор:
butterscotchd3ci - 6 лет назад
-
0
-
-
С браузера зайдите
-
Автор:
baby boo - 6 лет назад
-
0
-
-
Изменить порядок интегрирования в двукратном интеграле это значит преобразовать данный интеграл так, чтобы внешний интеграл зависил от переменной у, а внутренний интеграл зависит от переменной х.Область интегрирования:D: 0 ≤ x ≤ 1 - изменение переменной х. √(1-x²) ≤ y ≤ (1-x)² - изменение переменной у.y = √(1-x²) ⇔ y² = 1- x² ⇔ x² + y² = 1 - уравнение окружности с центром (0;0) и радиусом R = 1 и при этом y ≥ 0.

-
Автор:
casio - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
В какой стране была создана ПАЭС? Беларусь, где именно?
-
Предмет:
Беларуская мова -
Автор:
gretel - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- Колонизация бессарабии заселенные народы.
-
Эти листья прошлогодние, они перезимовали под снегом.
Объясните, почему поставлена запятая перед словом "они".-
Предмет:
Русский язык -
Автор:
vincent49 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Помогите пожалуйста решить задачку! Затрачивая 0.9 ч на одну деталь бригада изготавливает 540 деталей за смену. Сколько деталей изготовит бригада за смену, если будет делать одну деталь за 0.6 что? Н а сколько процентов при этом повеситься производительность? Решите, составив пропорцию.
-
Предмет:
Математика -
Автор:
grant6 - 6 лет назад
-
Ответов:
5 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
