Задать вопрос Регистрация
Помочь другим

  • Исследовать сходимость , абсолютную сходимость и расходимость.

    ДАЮ 100 БАЛЛОВ! СРОЧНА!!!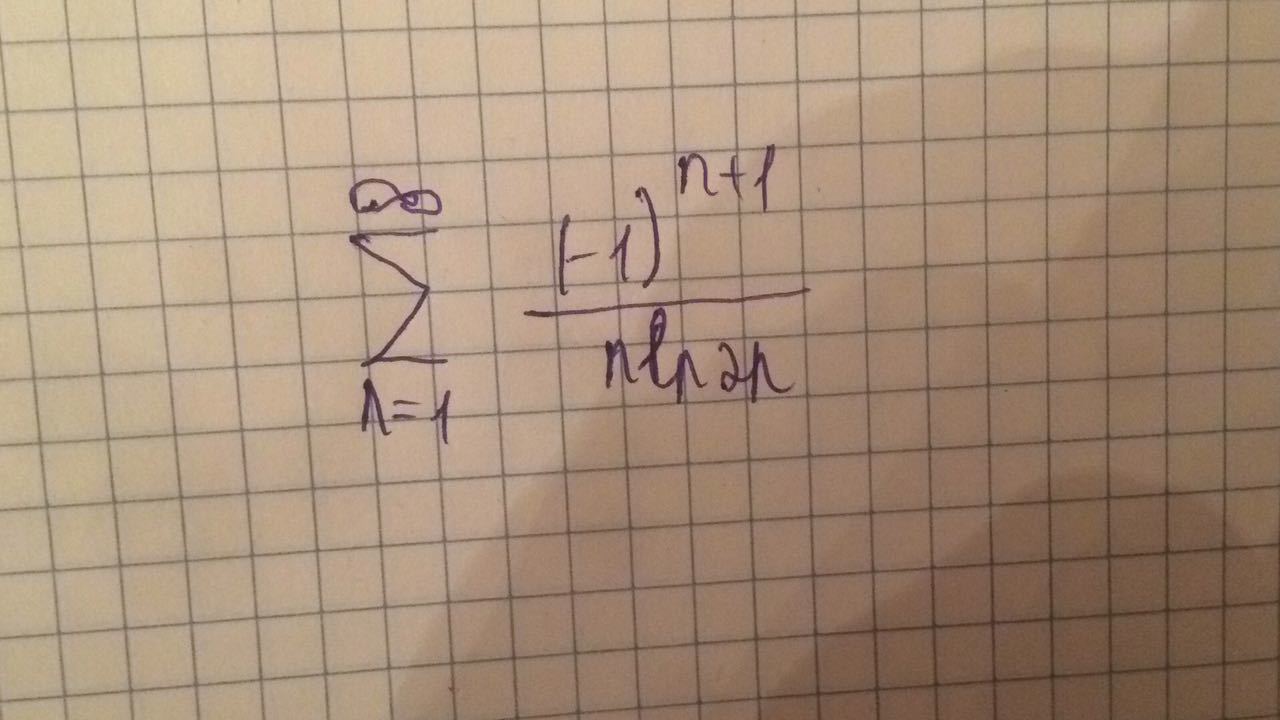

    question img

Ответы 2

  • https://znanija.com/task/28419645
  • Первое условие признака Лейбница выполняется 1/ln2 > 1/ln8 > 1/ln216 \lim_{n \to \infty} \frac{1}{n\ln 2n} =0Второе условие Лейбница выполняется. Таким образом, рассматриваемый ряд сходится.Исследуем теперь ряд на абсолютность. Возьмём ряд по модулю\displaystyle \sum^{\infty}_{n=1}\bigg| \frac{(-1)^{n+1}}{n\ln 2n}\bigg|=\displaystyle \sum^{\infty}_{n=1} \frac{1}{n\ln 2n} Применим интегральный признак:  \displaystyle \int\limits^{\infty}_1 {} \, \frac{dn}{n\ln 2n}=2 \int\limits^{\infty}_1 \frac{d\ln 2n}{\ln 2n} =2\ln|\ln 2n|\bigg|^{\infty}_1=\infty Несобственный интеграл расходится, следовательно и ряд по модулю тоже расходится, а значит данный ряд будет сходится УСЛОВНО   

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years