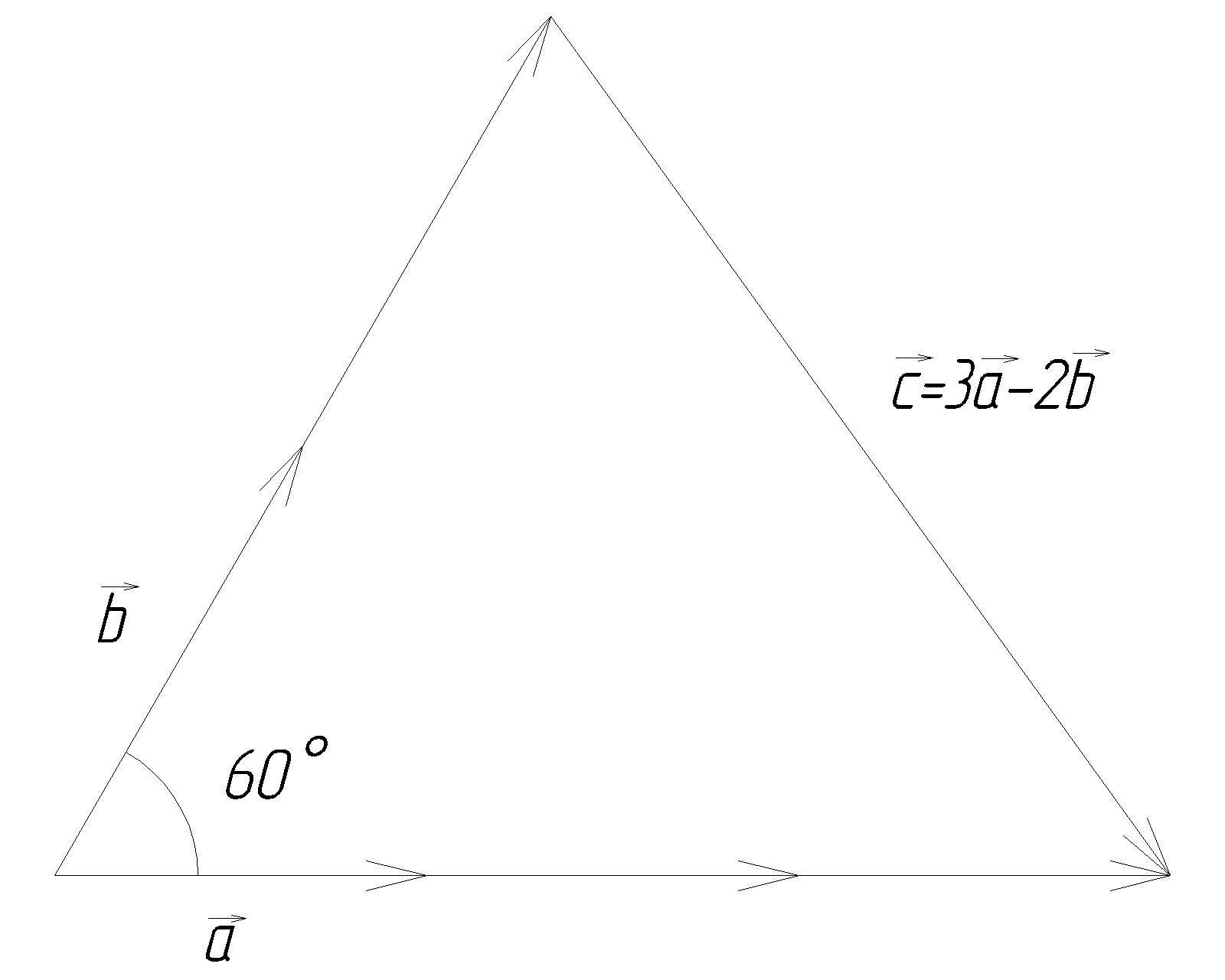
даны векторы a и b которые образуют угол 60 градусов. найти длину вектора c=3а-2b, если длина |a|=3, |b|=4

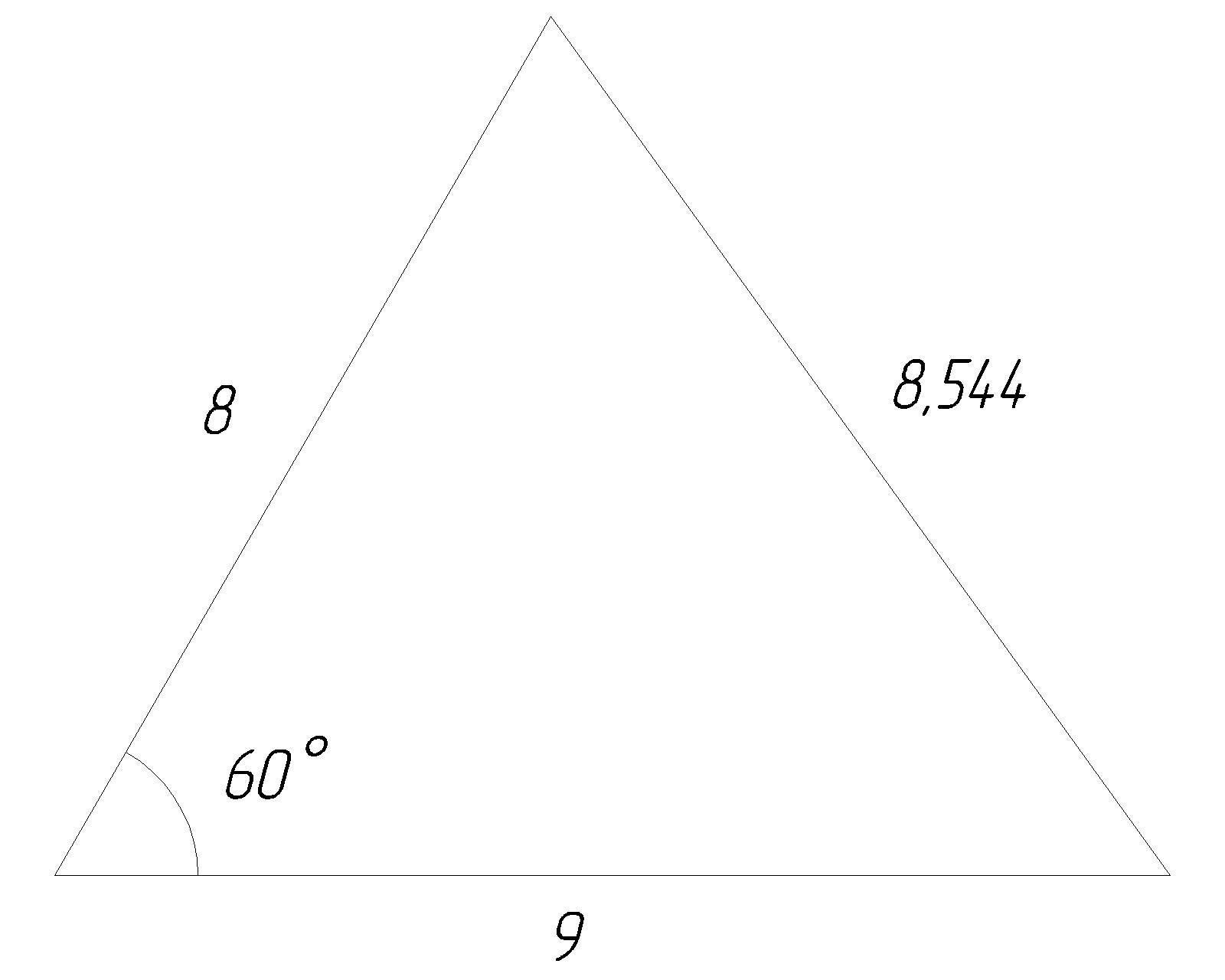
Добавил поясняющий рисунок.Модуль вектора 3a в 3 раза больше модуля вектора a:|\;3\vec a\;| = 3\cdot |\;\vec a\;| = 3\cdot3=9Модуль вектора 2b в 2 раза больше модуля вектора b:|\;2\vec b\;| = 2\cdot |\;\vec b\;| = 2\cdot4=8Направление вектора c определяется правилом вычитания векторов. Часто его запоминают так: из какого вектора вычитаем, к его концу и направлен результирующий вектор. В полученном треугольнике сторону, лежащую напротив угла в 60 градусов (т.е. модуль вектора c), можно найти по теореме косинусов:|\;\vec c\;|^{2}=|\;3\vec a\;|^{2}+|\;2\vec b\;|^{2}-2\cdot|\;3\vec a\;|\cdot|\;2\vec b\;|\cdot cos(60^{\circ}) \\ |\;\vec c\;|^{2}=9^{2}+8^{2}-2\cdot9\cdot8\cdot 0,5 \\ |\;\vec c\;|^{2}=81+64-72 \\ |\;\vec c\;|^{2}=73 \\ |\;\vec c\;|=\sqrt{73} \\ |\;\vec c\;|\approx8,544Также я добавил рисунок-результат.