-
Вычислить производные первого порядка указанных функций:
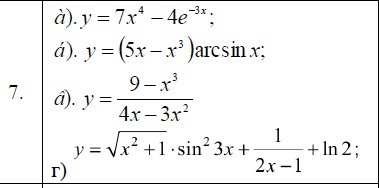
-
Предмет:
Математика -
Автор:
alanawarren - 6 лет назад
-
Ответы 3
-
Спасибо большое!Чтоб я без вас делал)))))
-
Автор:
shamarpetty - 6 лет назад
-
0
-
-
-
Автор:
clayton - 6 лет назад
-
0
-
-
-
Автор:
ryland - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найдите слово со значением: "ОТСУТСТВИЕ ТВЕРДОСТИ В РЕШЕНИИ ПРОБЛЕМЫ"
Ловкость и наглость кота довели обитателей квартиры до малодушного решения: избавиться от надоедливого животного.-
Предмет:
Русский язык -
Автор:
bobos0ef - 6 лет назад
-
Ответов:
4 -
Смотреть
-
- план характеристики страны индии(географическое положение, границы.Оценка географического положения страны)
-
В двух кусках 24м сукна. Один кусок стойт 2400тг а другой 4800тг. Сколько метров сукна в каждом куске
-
Предмет:
Математика -
Автор:
adrianaford - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Черчение... помогите найти технический чертеж каждого из деталей ...
-
Предмет:
Другие предметы -
Автор:
manuel - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
