Задать вопрос Регистрация
Помочь другим

  • Найти общее решение дифференциального уравнения 2-го
    порядка.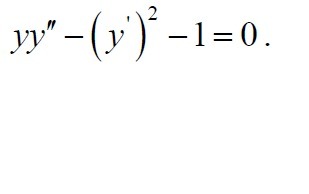

    question img

Ответы 1

  • Это дифференциальное уравнение второго порядка, независящее явным образом от неизвестной переменной х. Данное уравнение имеет вид y''=f(y,y').Вводим новую функцию p(y). Положим y'=p(y), тогда y''=pp'В результате имеем, чтоypp'-p^2-1=0 - уравнение с разделяющимися переменными\displaystyle \frac{dp}{dy} = \frac{p^2+1}{py} ~~~\Rightarrow~~~ \frac{pdp}{p^2+1} = \frac{dy}{y} Проинтегрируем обе части последнее равенство , получим\displaystyle \frac{1}{2} \int \frac{d(p^2+1)}{p^2+1} =\int \frac{dy}{y} ~~~\Rightarrow~~~ 0.5\ln(p^2+1)=\ln|y|+\lnC\\ \\ \sqrt{p^2+1} =C_1y~~~\Rightarrow~~~ p^2=C_1y^2-1Тогда, выполнив обратную замену, получимy'= \pm\sqrt{C_1y^2-1}\\ \\ \dfrac{dy}{ \sqrt{C_1y^2-1} } =\pm dx Интегрируя получим                     \dfrac{1}{ \sqrt{C_1} } \ln| \sqrt{C_1y^2-C_1}+C_1y| =\pm x+C_2 - общий интеграл

    • Автор:

      heraclio
    • 6 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years