Задать вопрос Регистрация
Помочь другим

  • Помогите пожалуйста
    Нужно найти общее решение дифференциального уравнения первого порядка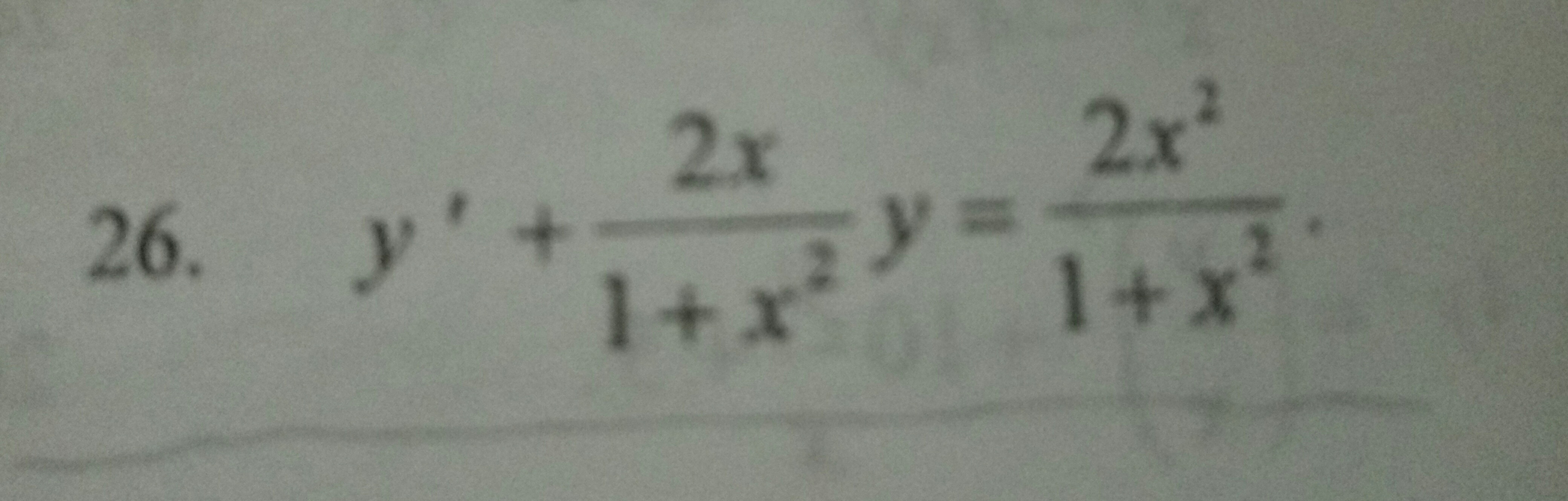

    question img

Ответы 1

  • уравнение вида:y'+P(x)y=Q(x)Называется линейным неоднородным дифференциальным уравнением первого порядка (или частным случаем уравнения Бернулли)Такие уравнения решаются либо методом вариации постоянной, либо методом Бернулли. Я покажу второй методРешение:y'+ \frac{2x}{1+x^2} y= \frac{2x^2}{1+x^2} \\ \\ Замена: y=uv;  y'=u'v+v'u, тогдаu'v+v'u+ \frac{2x}{1+x^2} uv= \frac{2x^2}{1+x^2} \\ \\ u'v+u(v'+ \frac{2x}{1+x^2}v)=\frac{2x^2}{1+x^2} \\ \\ v'+ \frac{2x}{1+x^2}v=0 \\ \\ \frac{dv}{dx} + \frac{2x}{1+x^2}v=0 \\ \\ \frac{dv}{dx} =- \frac{2x}{1+x^2}v \\ \\ \frac{dv}{v} =- \frac{2x}{1+x^2}dx \int\limits {\frac{dv}{v}}=- \int\limits {\frac{2x}{1+x^2} } \, dx \\ \\ ln|v|=- \int\limits {\frac{1}{1+x^2} } \, d(1+x^2) \\ \\ ln|v|=-ln|1+x^2| \\ \\ ln|v|=ln | \frac{1}{1+x^2} | \\ \\ v= \frac{1}{1+x^2}u'v+u(v'+ \frac{2x}{1+x^2}v)=\frac{2x^2}{1+x^2}Так как выражения в скобках приравнивалось к нулю, то остается:u'v=\frac{2x^2}{1+x^2}подставляем значение v:u'\frac{1}{1+x^2}=\frac{2x^2}{1+x^2} \ \ |*(1+x^2) \\ \\ u'=2x^2 \\ \\ u= \int\limits {2x^2} \, dx = \frac{2x^3}{3} +CИ наконец, обратная замена:y=uv=(\frac{2x^3}{3} +C)* \frac{1}{1+x^2} \\ \\ OTBET: \ y=(\frac{2x^3}{3} +C) \frac{1}{1+x^2}

    • Автор:

      leahhsxv
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years