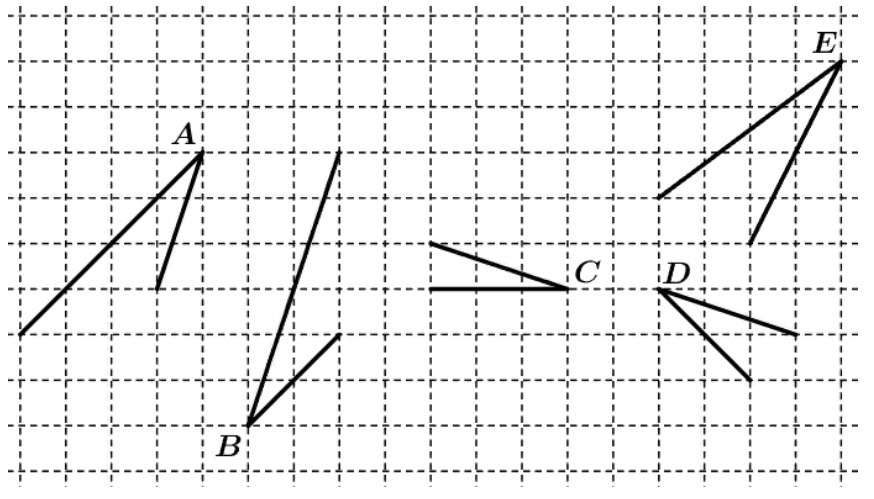
Какие из углов, изображённых на картинке, равны?

Какие из углов, изображённых на картинке, равны?
- Предмет:
  Математика
- Автор:
  louiehbdo
- 6 лет назад

Ответы 2

Ответ:
A,B,D,E
Пошаговое объяснение:
- Автор:
  braydon
- 6 лет назад
- 0
По внешнему виду определить, какие из углов равны, невозможно, если градусные меры углов близки по своим значениям. Нужно вычислять. Можно разными способами. Например, через скалярное произведение векторов можно найти косинусы углов и сравнить их.
$\vec a\cdot \vec b=|\vec a|\cdot |\vec b|\cdot \cos \hat{(\vec a; \vec b)}$
Произвольно построим прямоугольную систему координат XOY. Каждый изображённый угол образуют два вектора. Их координаты легко определить по узлам сетки. Например, координаты вектора $\vec m=\vec {MA}=(x_M-x_A;y_M-y_A)=(-5-(-4);1-4)=(-1;-3)$
1. ∠A; $\vec a(-1;-1);~~~\vec m(-1; -3)$
$\boldsymbol{\cos \angle A=}\cos \hat{(\vec a;\vec m)}=\dfrac {-1\cdot (-1)-1\cdot (-3)}{\sqrt{(-1)^2+(-1)^2}\sqrt{(-1)^2+(-3)^2}}=\boldsymbol{\dfrac 2{\sqrt5}}$
2. ∠B; $\vec b(1;3);~~~\vec n(1; 1)$
$\boldsymbol{\cos \angle B=}\cos \hat{(\vec b;\vec n)}=\dfrac {1\cdot 1+3\cdot 1}{\sqrt{1^2+3^2}\sqrt{1^2+1^2}}=\dfrac{4}{\sqrt{10}\sqrt{2}}=\boldsymbol{\dfrac 2{\sqrt5}}$
3. ∠C; $\vec c(-1;0);~~~\vec p(-3; 1)$
$\boldsymbol{\cos \angle C=}\cos \hat{(\vec c;\vec p)}=\dfrac {-1\cdot (-3)+0\cdot 1}{\sqrt{(-1)^2+0^2}\sqrt{(-3)^2+1^2}}=\boldsymbol{\dfrac 3{\sqrt{10}}}$
4. ∠D; $\vec d(3;-1);~~~\vec q(1; -1)$
$\boldsymbol{\cos \angle D=}\cos \hat{(\vec d;\vec q)}=\dfrac {3\cdot 1-1\cdot (-1)}{\sqrt{3^2+(-1)^2}\sqrt{1^2+(-1)^2}}=\boldsymbol{\dfrac 2{\sqrt5}}$
5. ∠E; $\vec e(-4;-3);~~~\vec k(-1; -2)$
$\boldsymbol{\cos \angle E=}\cos \hat{(\vec e;\vec k)}=\dfrac {-4\cdot (-1)-3\cdot (-2)}{\sqrt{(-4)^2+(-3)^2}\sqrt{(-1)^2+(-2)^2}}=\boldsymbol{\dfrac 2{\sqrt5}}$
cos ∠A = cos ∠B = cos ∠D = cos ∠E = $\boldsymbol{\dfrac 2{\sqrt5}}$
Ответ: ∠A = ∠B = ∠D = ∠E
- Автор:
  onyxsellers
- 6 лет назад
- 0
Добавить свой ответ