-
Heeelp
Кто-то умеет такое решать ?
Хотя бы одно ?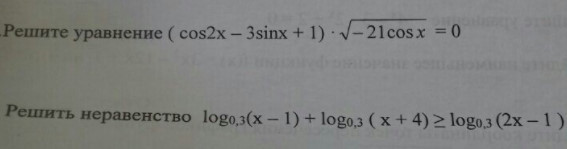
-
Предмет:
Математика -
Автор:
cameroncohen - 6 лет назад
-
Ответы 1
-
(cos2x - 3sinx+1)√(-21cosx)=0cos2x - 3sinx + 1=0 или √(-21cosx)=0при √(-21cosx)=0, т.е. -21cosx=0, cosx=0 ⇒ x=π/2 + πn, n∈Zпри cos2x - 3sinx + 1=0cos2x=1-2sin²x1-2sin²x-3sinx+1=02sin²x+3sinx=0sinx=a2a²+3a=0a(2a+3)=0a=0 или 2a+3=0sinx=0, x=π+πn, n∈Z2sinx+3=0sinx=-1,5, что невозможно, т.к. значения sin и cos расположены в диапазоне [-1;1]Ответы: x₁=π/2 + πn, n∈Z; x₂=π+πn, n∈Z
-
Автор:
raymond - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Антарктиду окружают шельфовые ледники. Самый большой - ледник Росса. Толщина ледника у суши 1 км 260 м, а у края, обращенному к морю - в 7 раз меньше. При этом над поверхностью моря видна лишь одна девятая часть ледяного барьера. На сколько метров ледяной барьер поднимается над морем?
-
Предмет:
Математика -
Автор:
sanaimccann - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
(7а+2б)^ -(3а-б) •(4а+5б) алгебра рішить
-
Предмет:
Алгебра -
Автор:
sneakersjhve - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Сочинение на тему (Попутчик,прохожий ).
-
Предмет:
Русский язык -
Автор:
anayasaunders - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
напишите маленький рефераот об жуке рогаче
-
Предмет:
Биология -
Автор:
lazarus8xh9 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
