Задать вопрос Регистрация
Помочь другим

  • Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям:

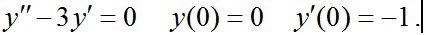
    question img

Ответы 1

  • Данное дифференциальное уравнение является однородным. Сделаем замену Эйлера y=e^{kx}, в результате чего получаем характеристическое уравнениеk^2-3k=0\\ k(k-3)=0\\ k_1=0;\\ k_2=3Общее решение однородного уравнения:  y=C_1+C_2e^{3x}y'=(C_1+C_2e^{3x})'=3C_2e^{3x}Осталось найти частное решение, подставляя начальные условия\displaystyle \left \{ {{0=C_1+C_2} \atop {-1=3C_2}} ight. ~~\Rightarrow~~~ \left \{ {{C_1=\frac{1}{3} } \atop {C_2=- \frac{1}{3} }} ight. Частное решение:   y=\frac{1}{3} -\frac{1}{3} e^{3x}

    • Автор:

      arelytlef
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years