-
помогите пожалуйста посчитать логарифмические и показательные уравнения
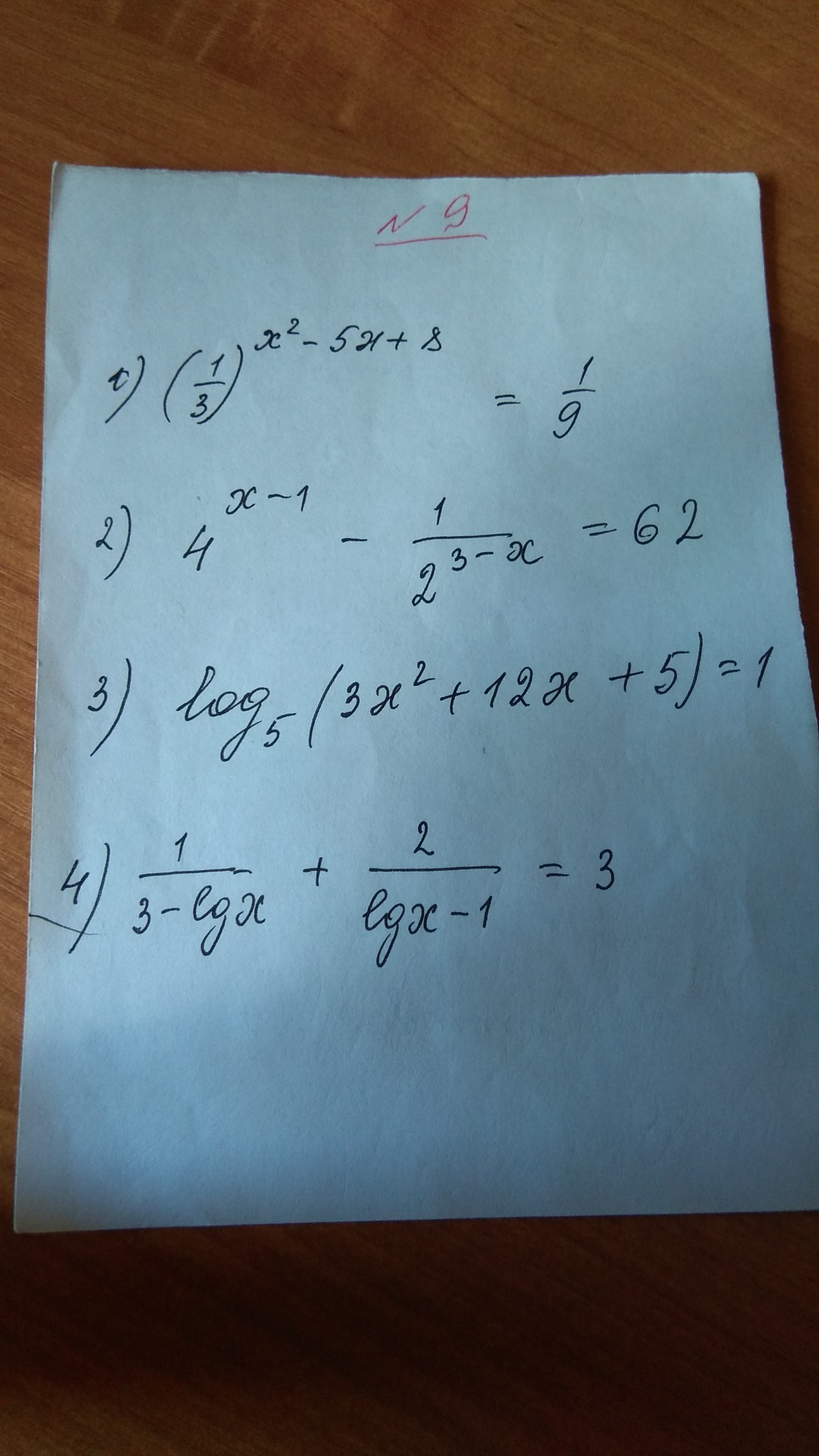
-
Предмет:
Математика -
Автор:
pablota0t - 6 лет назад
-
Ответы 1
-
1)(1/3)^(x^2-5x+8) = 1/9(1/3)^(x^2-5x+8) = (1/3)^2x^2 - 5x + 8 = 2x^2 - 5x + 6 = 0D = 5^2 - 4 6 = 25 - 24 = 1x1 = ( 5 - 1)/2 = 2x2 = ( 5 +1)/2 = 32)4^(x-1) - 1 / 2^(3-x) = 62[2^(x-1)]^2 - (1/4) 2^(x-1) = 62Обозначим 2^(x-1) = t > 0t^2 - t/4 - 62 = 0D = (1/4)^2 + 4 62 = 3969/16 = (63/4)^2t1 = (1/4 - 63/4)/2 < 0 - не удв. условию (t>0)t2 = (1/4 +63/4)/2 = 82^(x-1) = 82^(x-1)=2^3x-1=3x=43)log (5) (3x^2 + 12x + 5) = 1log (5) (3x^2 + 12x + 5) = log (5) (5)3x^2 + 12x + 5 = 53x(x + 4) = 0x1 = 0x2 = -43 x^2 + 12x + 5>0, т.к. находится в логарифме. Проверим:3 x1^2 + 12 x1 + 5 = 5 > 03x2^2 + 12 x2 + 5 = 5 > 0Ответ: x = 0, x = -44)Найдем допустимые значения:x>0 т.к. стоит в логарифменедопустимо: 3 - lg(x) = 03 = lg(x)3 lg(10) = lg(x)lg(10^3) = lg(x)x = 10^3недопустимо: lg(x) - 1 = 0lg(x) = 1lg(x) = lg(10)x= 10Теперь займемся уравнением:1 / (3 - lg(x) ) + 2 / (lg(x) - 1) = 3обозначим: lg(x) - 1 = t1 / (2 -t) + 2 / t = 3t + 2(2-t) = 3 t (2-t)t + 4 - 2t = 6t - 3t^23t^2 - 7t + 4 = 0D = 49 - 48 = 1t1 = (7 - 1)/6 = 1t2 = (7 + 1)/6 = 4/3lg(x) - 1 = t1lg(x) - 1 = 1lg(x) = 2lg(x) = 2 lg(10)lg(x) = lg(10^2)x = 10^2lg(x) - 1 = t2lg(x) - 1 = 4/3lg(x) = 7/3lg(x) = (7/3) lg(10)lg(x) = lg(10^(7/3))x = 10^(7/3)Ответ: x = 10^2, x = 10^(7/3)
-
Автор:
cristoferauif - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!
6 1/5 - 2 3/5
Буду очень благодарна,заранее спасибо :з-
Предмет:
Математика -
Автор:
valentina80 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Можно 5 толстых вопросов по сказке гадкий утёнок ?))) 3 Класс по чтению задание))
-
Предмет:
Литература -
Автор:
rex11 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
50 БАЛЛОВ
ЛИТЕРАТУРА.6 КЛАСС
Напиши сочинение на одну из тем:" верный друг", "друзья познаются в беде", "голос совести".-
Предмет:
Литература -
Автор:
elliot - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Определить относительную влажность воздуха при температуре 0*C, а содержание водного пара в воздухе 3г/м3
-
Предмет:
География -
Автор:
clancyoliver - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
