Задать вопрос Регистрация
Помочь другим

  • 16. Доказать методом математической индукции, что для любого n∈N...

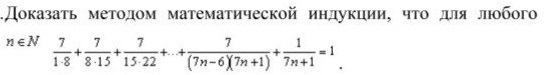
    question img

Ответы 1

  • 1) n = 1 \frac{7}{1 * 8} + \frac{1}{7+1} =1верно, это база2) предположим, что для n = k - верно \frac{7}{1*8} + \frac{7}{8+15} +...+ \frac{7}{(7k-6)(7k+1)} + \frac{1}{7k+1} =13) докажем, что для n = k+1 так же верно \frac{7}{1*8} + \frac{7}{8+15} +...+ \frac{7}{(7k-6)(7k+1)}=1 - \frac{1}{7k+1} \\\\ \frac{7}{1*8} + \frac{7}{8+15} +...+ \frac{7}{(7k-6)(7k+1)}+ \frac{7}{(7k+1)(7k+8)}+ \frac{1}{7k+8} =\\ =1- \frac{1}{7k+1} + \frac{7}{(7k+1)(7k+8)}+ \frac{1}{7k+8} =1 - \frac{7k+1-7k-8+7}{(7k+1)(7k+8)} =1верно, по ММИ доказано

    • Автор:

      grace93
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years