Найти общее решение системы дифференциального уравнения и выделить частное решение,

Найти общее решение системы дифференциального уравнения и выделить частное решение, удовлетворяющее начальным
условиям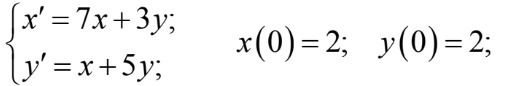
- Предмет:
  Математика
- Автор:
  miya
- 5 лет назад

Ответы 1

Продифференцируем первое уравнение, имеем $x''=7x'+3y'~~~\Rightarrow~~~ \frac{1}{3} x''-\frac{7}{3}x'=y'$ и $y=\frac{1}{3} x'-\frac{7}{3} x$ Подставляем все эти данные во второе уравнение, получим $\frac{1}{3} x''-\frac{7}{3} x'=x+5(\frac{1}{3} x'-\frac{7}{3} x)\\ \\ \frac{1}{3} x''-\frac{7}{3} x'=x+\frac{5}{3} x'-\frac{35}{3} x\\ \\ \frac{1}{3} x''-4x'+\frac{32}{3}x =0~~~|\cdot 3\\ \\ x''-12x'+32x=0$ последнее уравнение является дифференциальным уравнением с постоянными коэффициентами, однородным уравнение.Пусть $x=e^{kt}$ , тогда получим характеристическое уравнение: $k^2-12k+32=0\\ (k-6)^2-4=0\\ \\ k_1=4;~~~k _2=8$ $x=C_1e^{4t}+C_2e^{8t}$ Тогда $y=\frac{1}{3} (C_1e^{4t}+C_2e^{8t})'_t-\frac{7}{3} (C_1e^{4t}+C_2e^{8t})=\\ \\ = \frac{4}{3} C_1e^{4t}+\frac{8}{3} C_2e^{8t}-\frac{28}{3} C_1e^{4t}-\frac{56}{3} C_2e^{8t}=-8C_1e^{4t}-16C_2e^{8t}$ Найдем теперь частное решение, подставляя начальные условия $\displaystyle \left \{ {{2=C_1+C_2} \atop {2=-8C_1-16C_2}} ight. ~~~\Rightarrow~~~ \left \{ {{16=8C_1+8C_2} \atop {2=-8C_1-16C_2}} ight. \\ \\ \\ 18=-8C_2~~~\Rightarrow~~~ C_2=-2.25\\ \\ C_1=2-C_2=2+2.25=4.25$ Частное решение: $\boxed{x=4.25e^{4t}-2.25e^{8t}}$ и $\boxed{y=-34e^{4t}+36e^{8t}}$
- Автор:
  edwardbx8b
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

Найти общее решение системы дифференциального уравнения и выделить частное решение, удовлетворяющее начальным условиям

Ответы 1

Топ пользователей

Найти общее решение системы дифференциального уравнения и выделить частное решение, удовлетворяющее начальным
условиям