-
Решите неравенство. Номер 15 в ЕГЭ по профильной математике
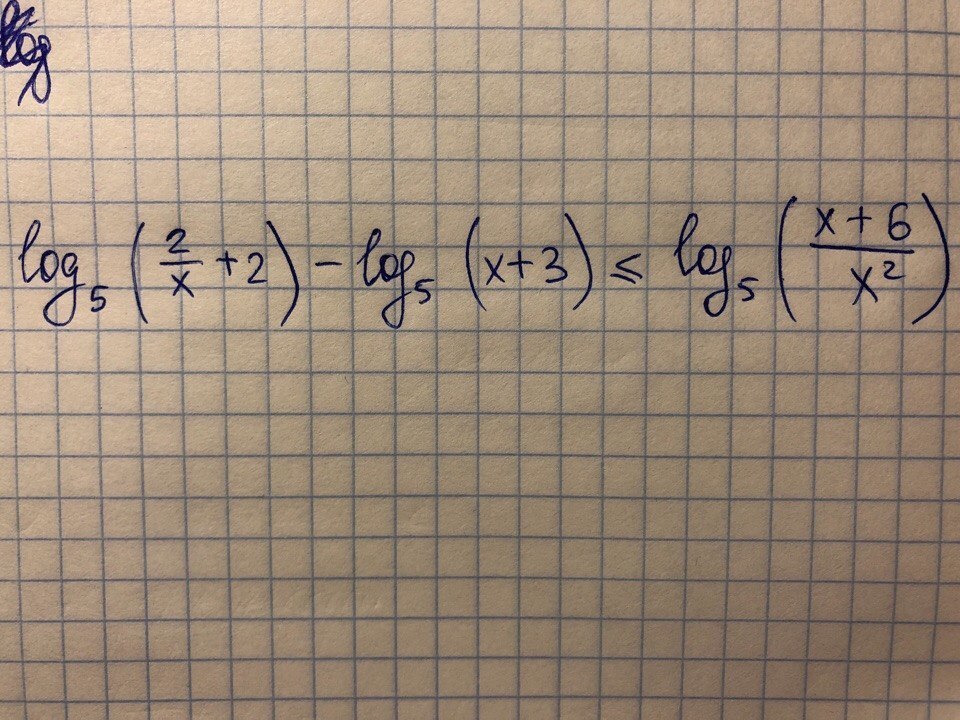
-
Предмет:
Математика -
Автор:
bogey - 6 лет назад
-
Ответы 2
Еще вопросы
-
Помогите найти период функции:y=2sin2x
-
Предмет:
Математика -
Автор:
bootie - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
большая коробка конфет в 2 раза дороже маленькой хотят купить 3 большие коробки и две маленькие Но если купить две большие и 3 маленькие коробки то покупка будет дешевле на 60 руб. сколько стоит карта коробка конфет
-
Предмет:
География -
Автор:
kobaroberson - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
ОГРОМНАЯ ПРОСЬБА ПЖ ПОМОГИТЕ . СЕГОДНЯ НА 3 ЗАДАНИЕ ЕГЭ. У МЕНЯ БЫЛ ТАКИЕ ЖЕ УСЛОВИЯ И ТАКОЙ ЖЕ РИСУНОК (КАК НА ФОТО) НО НА ЭКЗАМЕНЕ У ЭТОГО РИСУНКА Верх был слева а вниз справа(имеет ли это какое-нибудь значение?)
кто знает как решается скиньте ответ . спс большое :)-
Предмет:
Математика -
Автор:
natalie15 - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
На основе рекурсивного алгоритма построить изображение(в паскале). Программа, выполняющая построение, должна быть инвариантна относительно начальных координат и числа итераций., изобр ниже
Умоляю, помогите с этим заданием срочненько нужно(-
Предмет:
Информатика -
Автор:
foxy78 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years

