-
При каких значениях параметра а система имеет 4 различных решения?
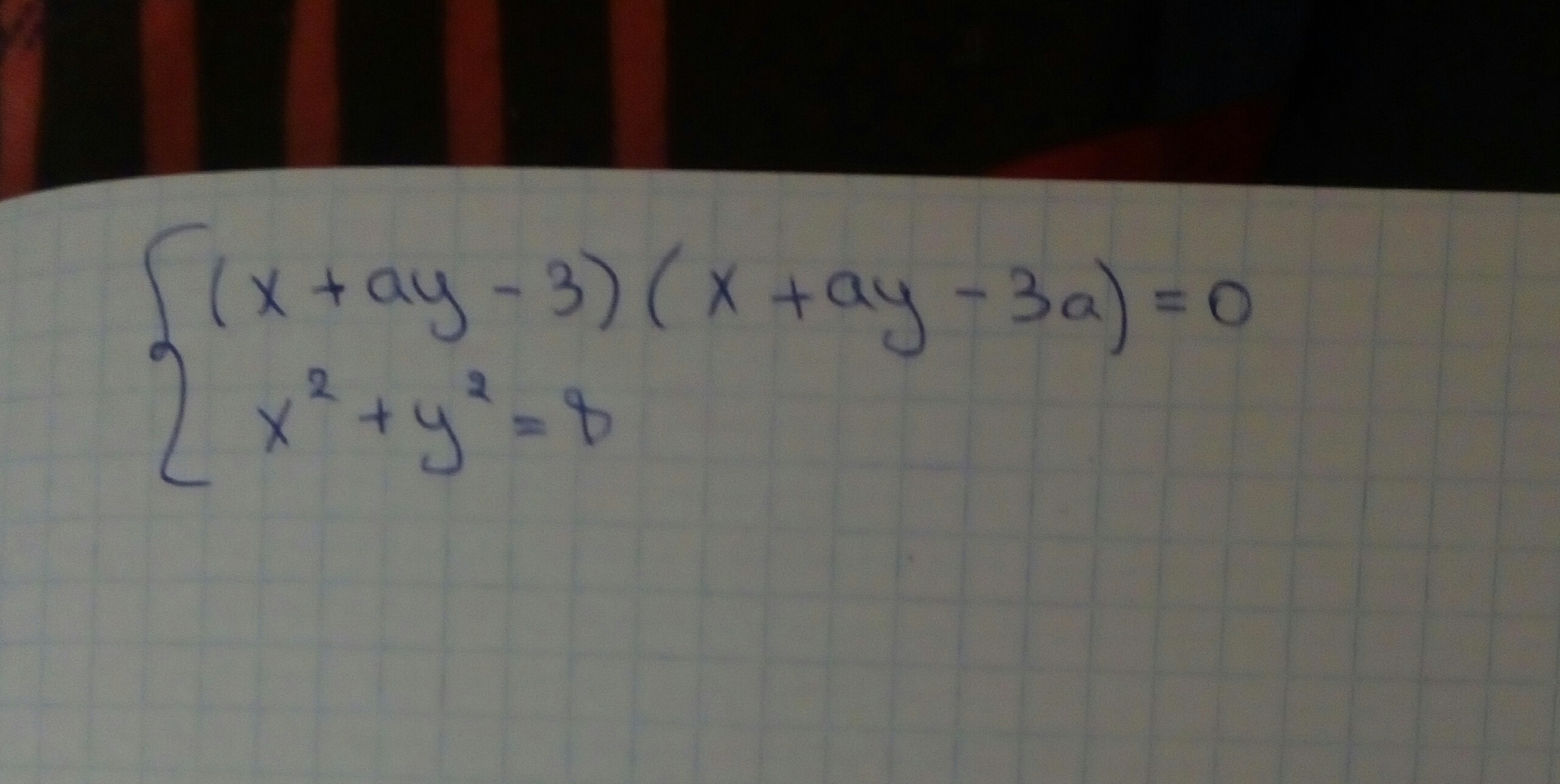
-
Предмет:
Математика -
Автор:
cowboy - 6 лет назад
-
Ответы 1
-
При каких значениях параметра а система имеет 4 различных решения?
Решение:Так как в первом уравнение системы произведение то система уравнений распадается на две подсистемы.
Каждая система уравнений представляет собой прямую x+ay-3=0(x+ay-3a=0) и окружность x²+y²=8 с центров в начале координат и радиусом R=2√2.Легко показать что при а=0 данные система имеет только два решения так как первое уравнение в первой системе x=3 и первая система решений не имеет, а во второй системе первое уравнение х = 0 и система имеет два решения.Поэтому для четырех решений необходимо чтобы каждая подсистема уравнений имела 2 решения и a≠0.
В первой системе уравнений подставим первое уравнение во второе (3 - ay)² + y² = 8 9 - 6ay+a²y² +y² = 8 y²(a² + 1) - 6ay + 1 = 0Данное уравнение имеет два решения если дискриминант больше нуля D > 0D = 36a² - 4(a² + 1) = 36a² - 4a² - 4 = 32a² - 4 = 4(8a²-1) 8a² - 1 > 0 a² > 1/8 если a ∈ (-oo;-1/(2√2))U(1/(2√2);+oo)Во второй системе подставим первое уравнение во второе (3a - ay)²+ y² = 8 9a² - 6a²y + a²y² + y² = 8 y²(a² + 1) - 6a²x + 9a² - 8 =0Данное уравнение имеет два решения если дискриминант больше нуля D>0D = 36a⁴ - 4(a²+1)(9a²-8) = 36a⁴ - 4(9a⁴+a²-8)=36a⁴ - 36a⁴ -4a² +32== 32 - 4a² =4(8 - a²) 8 - a² > 0 a² < 8 если a∈(-2√2;2√2)Пересечение интервалов решений двух систем уравнений является интервал a∈(-2√2;-1/(2√2))U(1/(2√2);2√2)Ответ :a∈(-2√2;-1/(2√2))U(1/(2√2);2√2)
-
Автор:
timmydlln - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
(arccos(-1))/(arcsin((1)/(3))+arccos((1)/(3)))
-
Предмет:
Математика -
Автор:
cadennuzg - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Однажды я смотрел фильм и услышал музыку Свиридова красивую и мелодичную. Это и есть те звуки и нити, которые помогают человеку не забывать то прекрасное что есть на земле. Музыка, может быть, самое прекрасное что есть у нас. Только композитор может понять, что волнует человека и передать все чувства, которые испытывают люди. Люди, слушая музыку плачут, жалеют себя. Музыка — это и есть самое восхитительное в жизни, человека которая помогает открывать для себя что-то необыкновенное, чистое. Музыка и природа не дает человеку одичать. Недавно я побывал на родине Свиридова в Курской области и понял, что эта природа подарила композитору замечательные звуки. Помогите выявить проблему которую ставит автор? 3 проблемы
-
Предмет:
Русский язык -
Автор:
emmanuel43 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Средняя кинетическая энергия молекул газа 1.5*10^-20 Дж. Определить температуру газа.
-
Предмет:
Физика -
Автор:
mckinleyburch - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Закончи предложение, выбрав правильный вариант ответа: Две параллельные плоскости пространство делят на *
1 балл
четыре части
три части
шесть частей
две части-
Предмет:
Математика -
Автор:
semajacfp - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
