-
Докажите, что если 1/a + 1/b + 1/c = 1/(a+b+c), то
1/a^3 + 1/b^3 + 1/c^3 = 1/(a^3 + b^3 + c^3)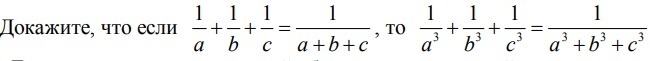
-
Предмет:
Математика -
Автор:
mariano - 6 лет назад
-
Ответы 6
-
Помогите плиз
-
Автор:
kingvalenzuela - 6 лет назад
-
0
-
-
Нелии
-
Автор:
guccicannon - 6 лет назад
-
0
-
-
https://znanija.com/task/29289079
-
Автор:
cannolilaht - 6 лет назад
-
0
-
-
Ээто оч важно прошу моя оценка зависит от этого плииз это последний номер в моих добавленных заданиях
-
Автор:
astro10ev - 6 лет назад
-
0
-
-
https://znanija.com/task/29289079
-
Автор:
zara78 - 6 лет назад
-
0
-
-
Если a = -b, то утверждение очевидно. Пусть a ≠ -b. Найдём c из первого равенства.1/a + 1/b = 1/(a + b + c) - 1/c(a + b)/(ab) = -(a + b)/(c (a + b + c)) – делим обе части уравнения на (a + b) ≠ 01/(ab) = -1/(c (a + b + c))c^2 + (a + b) c + ab = 0По теореме Виета сумма корней этого уравнения равна -(a + b), произведение ab. Очевидно, c = -a или c = -b. Но тогда опять-таки выполнение второго равенства очевидно.
-
Автор:
deshawn - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
с какого энергетического слоя начинается внешний энергетический уровень
СРОЧНО-
Предмет:
Химия -
Автор:
rainbow5kdc - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- znso4+nh4oh помогите пожалуйста
-
Помогите решить пожалуйста!!!максимум баллов дам( 2 и 3 задание)
-
Предмет:
Математика -
Автор:
nancy4xmv - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
метан может быть получен в лаборатории из:
1) карбид алюминия
2) ацетилид кальция calciumacetylide
3)формальдегид
4)метанол-
Предмет:
Химия -
Автор:
lewissavage - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
