Задать вопрос Регистрация
Помочь другим

  • Дана функция z=f(x;y). Показать, что она удовлетворяет данному уравнению.

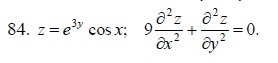
    question img

Ответы 1

  • Найдем первую и вторую частную производную по х (у-const).\displaystyle \frac{\partial z}{\partial x}= \frac{\partial(e^{3y}\cos x)}{\partial x}=-e^{3y} \sin x\\ \\ \frac{\partial^2 z}{\partial x^2}= \frac{\partial(-e^{3y}\sin x)}{\partial x} =-e^{3y}\cos x Найдем первую и вторую частную производную по y (x-const).\displaystyle \frac{\partial z}{\partial y}= \frac{\partial(e^{3y}\cos x)}{\partial y} =3e^{3y}\cos x\\ \\ \frac{\partial^2z}{\partial y^2}= \frac{\partial(3e^{3y}\cos x)}{\partial y} =9e^{3y}\cos x Подставив в условие, получим9\cdot \bigg(-e^{3y}\cos x\bigg)+9e^{3y}\cos x=0\\ \\ 0=0Что и требовалось показать )

    • Автор:

      baron84
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years