Задать вопрос Регистрация
Помочь другим

  • Решите, пожалуйста, эти два примера.Мне нужна с ними помощь.

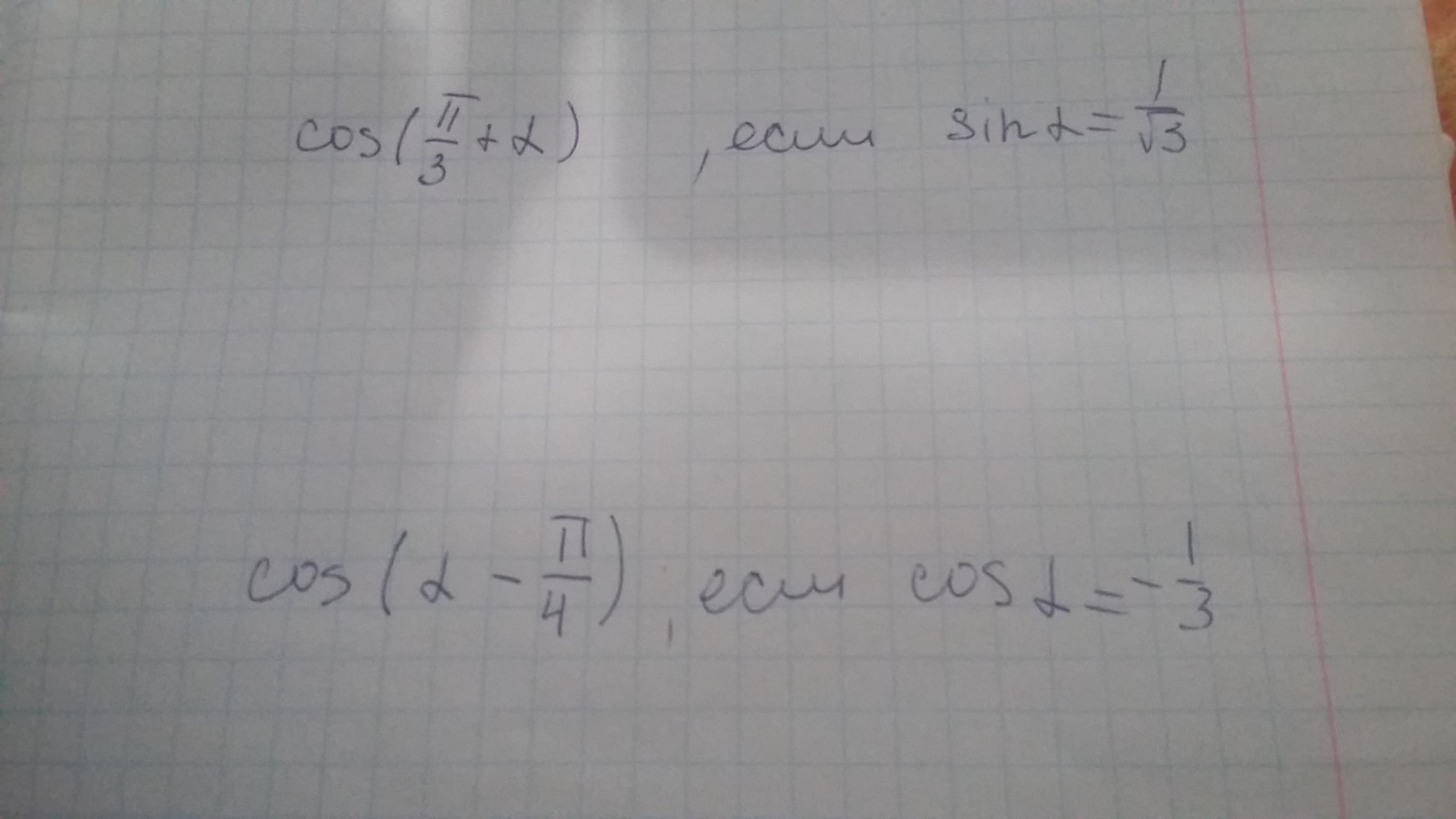
    question img

Ответы 1

  • 1.а) По формуле косинус суммы получаем:cos( \frac{ \pi }{3}+ \alpha ) = cos \frac{ \pi }{3} *cos \alpha -sin \frac{ \pi }{3}*sin \alpha = \frac{1}{2} *cos \alpha - \frac{ \sqrt{3} }{2} *sin \alpha б) Воспользуемся основным тригонометрическим тождеством: cos^ 2\alpha +sin^2 \alpha = 1 \\ cos^2 \alpha = 1-sin^2 \alpha \\ cos^2 \alpha = 1 - (\frac{1}{ \sqrt{3} })^2 \\ cos^2 \alpha = \frac{ 2 }{3} \\ \\ cos \alpha = \frac{ \sqrt{6} }{3} \\ cos \alpha = -\frac{ \sqrt{6} }{3}α находится в промежутке от 0 до π/2 (1-ая четверть). Из этого следует, что  значение косинуса на этом промежутке будет положительным.в) Подставляем вместо синуса и косинуса соответствующие им значения:\frac{1}{2} *cos \alpha - \frac{ \sqrt{3} }{2} *sin \alpha = \frac{1}{2}* \frac{ \sqrt{6} }{3}- \frac { \sqrt{3} }2} * \frac{1}{ \sqrt{3} } = \frac{1}{2}* \frac{ \sqrt{6} }{3}- \frac {1 }2} = \\ = \frac{1}{2}( \frac{ \sqrt{6} }{3} -1) 2. а) По формуле косинус разности получаем:cos( \frac{ \pi }{4}- \alpha ) = cos \frac{ \pi }{4}*cos \alpha +sin\frac{ \pi }{4}*sin \alpha = \frac{ \sqrt{2} }{2}*cos \alpha + \frac{ \sqrt{2} }{2} * sin \alpha  б) Аналогично первой задаче находим значение синуса, а так как  π/2<α<π, синус будет отрицательным.sin^2 \alpha =1- \frac{1}{9} = \frac{2 \sqrt{2} }{3} \\ sin \alpha = -\frac{2 \sqrt{2} }{3}в)\frac{ \sqrt{2} }{2}*cos \alpha + \frac{ \sqrt{2} }{2} * sin \alpha = \frac{ \sqrt{2} }{2} * (-\frac{1}{3}) + \frac{ \sqrt{2} }{2}*(- \frac{2 \sqrt{2} }{3} = - \frac{1}{3}*\frac{ \sqrt{2} }{2}-2* \frac{1}{3} = \\ = - \frac{1}{3} (\frac{ \sqrt{2} }{2}+2)

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years