-
Решите пожалуйста. На фото логарифмическое неравенство))
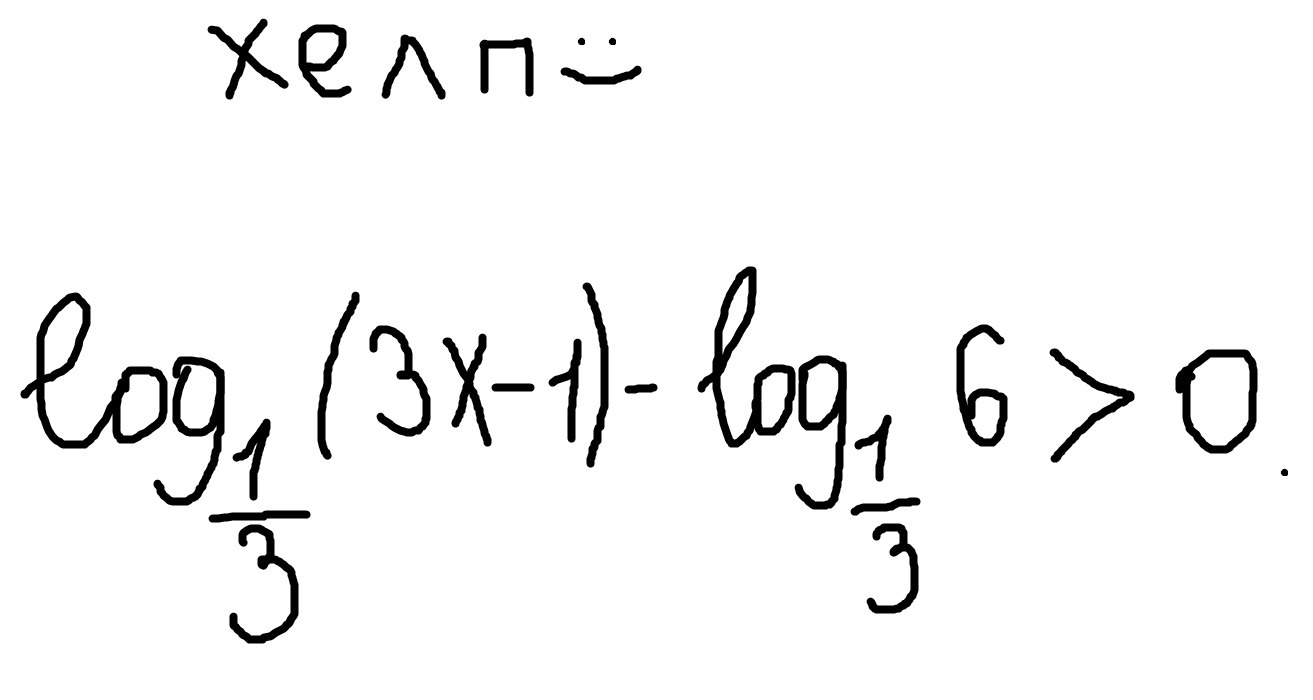
-
Предмет:
Математика -
Автор:
bugseypatel - 6 лет назад
-
Ответы 2
-
x€(1/3;7/3)
-
Автор:
maximiliano - 6 лет назад
-
0
-
-
После нахождения ОДЗ, получим что x>
;Перенести постоянную в правую часть и сменить её знак:㏒
(3x-1)>㏒
(6);Для 0<a<1 выражение ㏒a (x)>㏒a (b)=x<b:3x-1<6;Перенести постоянную в правую часть и сменить её знак:3x<6+1;Сложить число после знака неравенства:3x<7;Разделить обе части неравенства на 3:x<
,x>
;Найти пересечение множества решений и области допустимых значений:x∈{
,
}
-
Автор:
lucy40 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
СРОЧНО ФИЗИКА!!!В чем разница между молекулами льда, воды и водяного пара?
-
Предмет:
Физика -
Автор:
queenfarley - 6 лет назад
-
Ответов:
7 -
Смотреть
-
-
осевое сечение цилиндра является квадрат площадь которого равна 144 см^3. Найти объем цилиндра
-
Предмет:
Геометрия -
Автор:
lizethbxhy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Найдите наибольшее и наименьшее значение функции на данном промежутке.
f(x)=(x^2+5)/(x-2) , на промежутке [3;6] -
Определите,какой угол образуется с осью х касательная ,проведённая к графику функции...
-
Предмет:
Математика -
Автор:
kokoczpo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
