-
На рисунке изображен график производной функции f(x), определенной на интервале (-14;9).
Найдите количество точек максимума функции f(x) на отрезке [-12 ;7]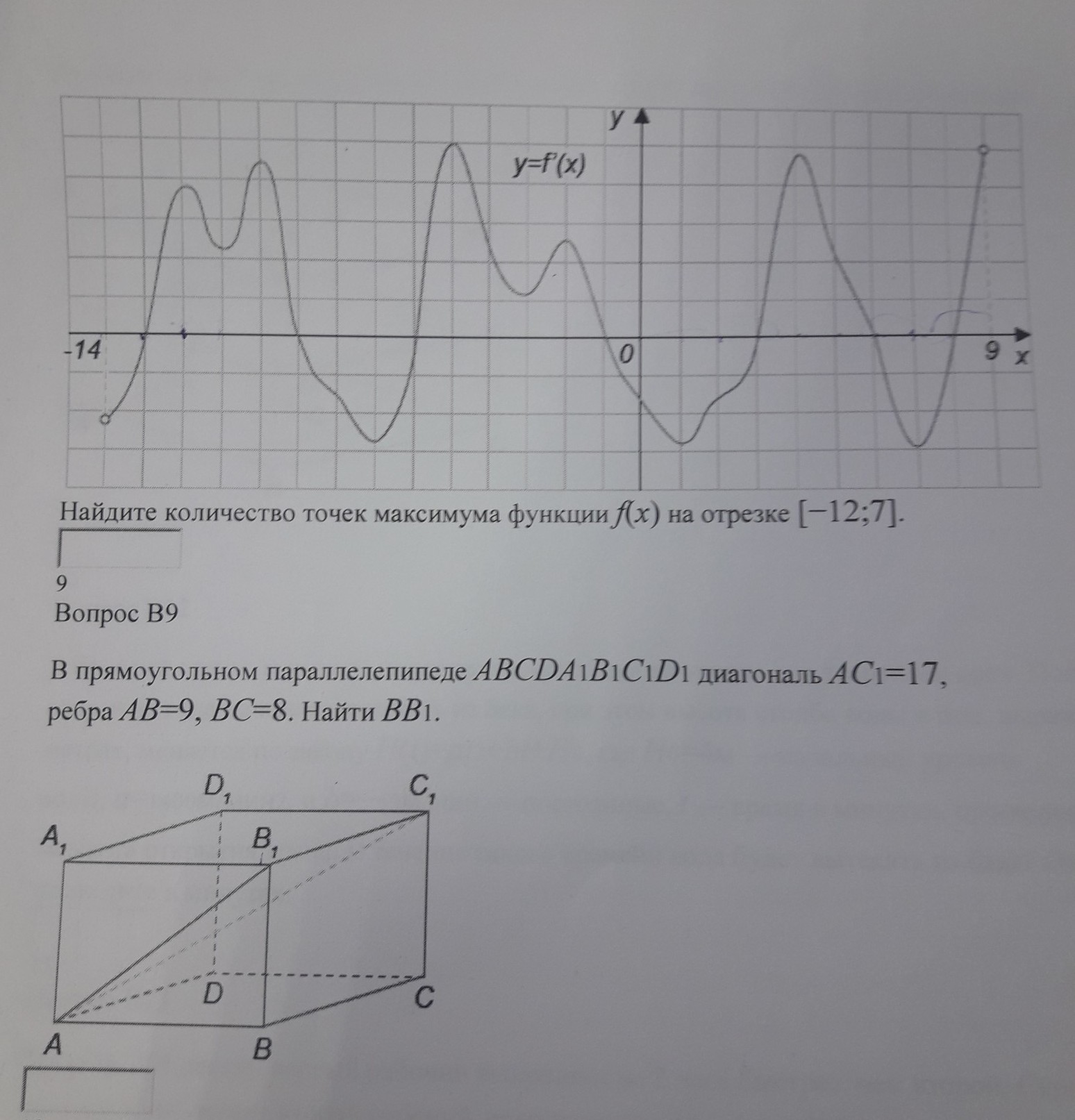
-
Предмет:
Математика -
Автор:
panther - 6 лет назад
-
Ответы 2
-
большое спвсибо за пояснение
-
Автор:
deshawnrosales - 6 лет назад
-
0
-
-
1) В точках максимума производная = 0 . Таких точек на отрезке [-12,7] пять. Но производная должна при этом изменять знак с (+) на (-), то есть график должен проходить из верхней полуплоскости (там y'>0) в нижнюю (там y'<0). Таких точек три. См. рисунок.2) В1С1=ВС=8 ΔАВ1С1: ∠АВ1С1=90°, т.к. АВ1⊥В1С1. (В1С1⊥ грани АВВ1А1 , т.к. В1С1⊥А1В1 и В1С1⊥ВВ1; значит В1С1 ⊥ любой прямой, лежащей в этой грани) АВ1=√(АС1²-В1С1²)=√(17²-8²)=√225=15 (по теореме Пифагора). ΔАВ1В: ∠АВВ1=90° , т.к. АВ⊥ВВ1, как стороны прямоугольника, ВВ1=√(АВ1²-АВ²)=√(15²-9²)=√144=12

-
Автор:
toby45 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Сторона основания правильной четырёхугольной пирамиды равно 6м угол между боковым ребром и плоскостью основания 30 градусов. Найти площадь сечения проведённого через два боковых ребра, не лежащих в одной грани.
-
Предмет:
Математика -
Автор:
oompa loompanpj1 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Кто нибудь помогите пожалуйста найти решение диф. уравнения
-
Предмет:
Математика -
Автор:
terrell - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Определить параметр LC колебательного контура если резонансная частота равна 100кгц, а характеристическое сопротивление 20 Ом
-
Предмет:
Другие предметы -
Автор:
tickles - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
культура создаваемая анонимными творцами,называется А)элитарной Б) массовой В)народной Г)духовной
-
Предмет:
Обществознание -
Автор:
floyd38 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
