-
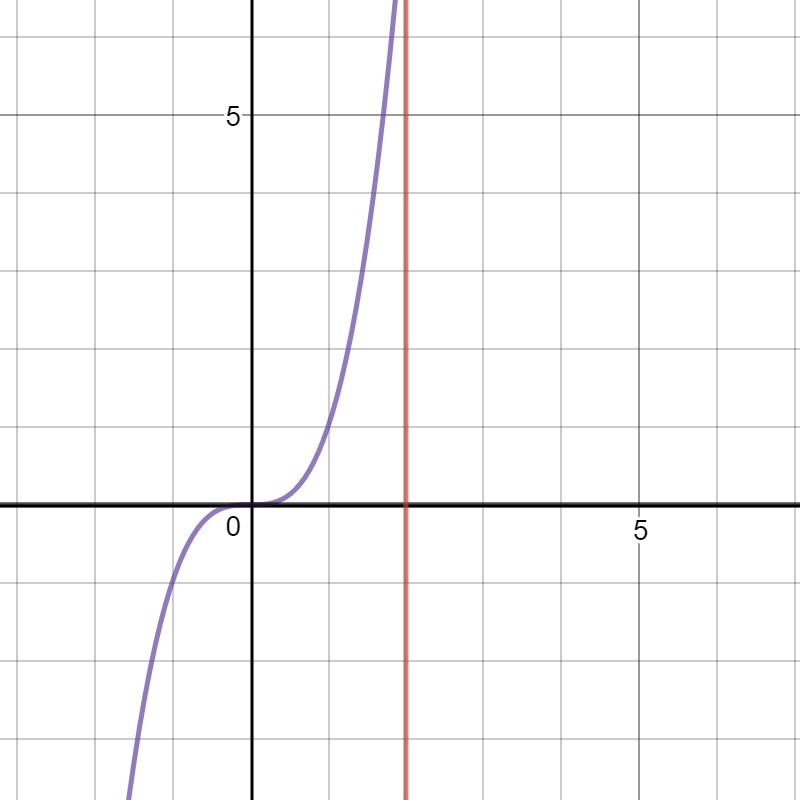
Вычислить двойной интеграл.[tex] \int\limits\,\int\limits_D {xy} \, dxdy, D: y=x^3, y=0, x=2 [/tex]
-
Предмет:
Математика -
Автор:
lillienorton - 6 лет назад
-
Ответы 1
-
-
Автор:
hinton - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Найти производную функции
2x^3-3x+4e^2x
Пожалуйста-
Предмет:
Алгебра -
Автор:
savannahgood - 6 лет назад
-
Ответов:
2 -
Смотреть
-
- к порошку мела в пробирке добавьте 1-2 мл воды и энергично взболтайте. Укажите, что в полученной вами дисперсной системе "суспензия" является дисперсионной средой, а чт о дисперсной фазой? Разделяются ли со временем дисперсионная среда и дисперсная фаза в данной суспензии?
-
4. При помощи какой операционной системы нужно начинать реанимацию компьютера? Почему?
-
Предмет:
Информатика -
Автор:
tasha41 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
83 балла РЕШИТЕ ЗАДАЧУ ПО ФИЗИКЕ ВАРИАНТ ПОД ЦИФРОЙ 20
How much to ban the user?
1 hour
1 day
100 years
